矩阵论整理：线性空间与线性映射

这是我在学习严质彬老师的矩阵论的过程中所做笔记整理以及个人理解的第一部分，个人能力有限，在理解过程中难免出现误解或者错误，如果您在阅读过程中发现了问题欢迎在评论区中指出和交流。下面的整理大致按照严老师的讲课顺序进行，然后穿插一些我遇到的问题和理解，以及其他的知识的复习。

总结

我下方的所有定义，定理和解释最后的结果就是辅助你理解这张图

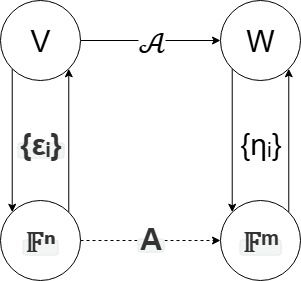
1. 上层：抽象世界

• V 和 W: 这是两个抽象的有限维线性空间。V 是定义域（输入空间），W 是上域（输出空间）。它们的“向量”可以是函数、多项式等任何抽象事物。
• 𝒜: V → W: 这是一个线性变换 (Linear Transformation)。它是一个从 V 到 W 的函数，并且保持线性结构（𝒜(u+v) = 𝒜(u)+𝒜(v) 且 𝒜(c·u) = c·𝒜(u)）。这是我们真正关心的、位于抽象世界的“动作”。

**2. 下层：具体世界 **

• 𝔽ⁿ 和 𝔽ᵐ: 这是我们熟悉的标准线性空间（坐标空间）。𝔽ⁿ 中的向量是 n×1 的列向量，𝔽ᵐ 中的向量是 m×1 的列向量。
• A: 这是一个 m × n 的矩阵。
• 从 𝔽ⁿ 到 𝔽ᵐ 的箭头: 这个动作是通过矩阵乘法实现的。输入一个 n×1 的坐标向量 x，通过左乘矩阵 A，得到一个 m×1 的输出坐标向量 y = Ax。这是我们能够实际计算的动作。

3. 左右两侧：

• V → 𝔽ⁿ (左侧向下的箭头): 这是坐标化的过程。通过为 V 空间选定一组基 {εᵢ} (ε₁, ..., εₙ)，我们可以将 V 中的任意一个抽象向量 v，唯一地“翻译”成 𝔽ⁿ 中的一个具体坐标向量 x。
• W → 𝔽ᵐ (右侧向下的箭头): 同样是坐标化。通过为 W 空间选定一组基 {ηᵢ} (η₁, ..., ηₘ)，我们可以将 W 中的任意一个抽象向量 w，“翻译”成 𝔽ᵐ 中的一个具体坐标向量 y。
• 𝔽ⁿ → V 和 𝔽ᵐ → W (向上的箭头): 这是反坐标化，即根据坐标和基，重构出原来的抽象向量。

预备知识

群环域

笛卡尔积

对于两个非空集合 A 和 B，它们的笛卡尔积，记作 A × B，是所有可能形成的有序对 (a, b) 的集合，其中第一个元素 a 来自集合 A，第二个元素 b 来自集合 B。A × B = { (a, b) | a ∈ A 且 b ∈ B }

定义1：抽象加法

给定非空集合V和域F，若存在映射σ: V × V → V，则称σ为V上的加法。记作**(V₁, V₂) ↦ σ(V₁, V₂)**

1. “给定非空集合V和域F，”
   • 非空集合V (Non-empty Set V): 这将是我们的“向量空间”。V 里的元素我们称之为“向量”，但它们可以是任何东西：几何箭头、多项式、函数、或者n元数组 (n-tuples) 等。关键是它不是空的，至少有一个元素。
   • 域F (Field F): 这是一个数字系统，里面的数可以进行加、减、乘、除（除以非零数）运算。最常见的例子是实数域 R 或复数域 C。F 里的元素我们称之为“标量”。
2. “若存在映射σ: V × V → V”
   • 映射 (Mapping): “映射”就是“函数”的另一种说法。它是一个规则，将一个集合（输入集/定义域）中的每个元素与另一个集合（输出集/到达域）中的一个确切元素对应起来。
   • V × V (笛卡尔积): 这是 V 与自身的笛卡尔积。它的每一个元素都是一个**有序对 (V₁, V₂) **，其中 V₁ 和 V₂ 都来自集合 V。所以，这个映射的输入是一对 V 中的元素。
   • → V (箭头指向V): 这表示映射的输出是一个单个的、且仍然属于集合 V 的元素。
   • 总结： 存在一个规则 (σ)，你给它两个 V 中的元素，它就能给你返回一个 V 中的元素。
3. “则称σ为V上的加法。”
   • 这就是核心结论。这个能接收两个V中元素并返回一个V中元素的映射 σ，我们就给它起个名字，叫做 V 上的**“加法”**。
4. “(V₁, V₂) ↦ σ(V₁, V₂)”
   • 这只是对上面映射 σ 的一种更具体的写法。
   • ↦ 符号读作 "maps to" (映射到)，这个符号用来连接集合中的元素，从微观上展示函数的具体运算规则。比如，x ↦ sin(x) 就说明了任意输入 x 都将被映射到其正弦值。→ 这个符号用来连接两个集合，即函数的定义域（输入集合）与到达域（输出集合）。例如，sin: ℝ → [-1, 1]
   • 它表示：有序对 (V₁, V₂) 被映射到了 σ(V₁, V₂) 这个结果上。
5. 类似的可以定义数乘操作

定义2：线性空间（向量空间）

设 V 是一个非空集合，其元素称为向量。设 F 是一个域（通常是实数域 ℝ 或复数域 ℂ），其元素称为标量。若在 V 中定义了以下两种运算：

1. 向量加法 (Vector Addition)
   一个映射 + : V × V → V，对于任意两个向量 u, v ∈ V，它们的和 u + v 仍然属于 V。
2. 标量乘法 (Scalar Multiplication)
   一个映射 · : F × V → V，对于任意标量 k ∈ F 和任意向量 v ∈ V，它们的积 kv 仍然属于 V。

并且，这两种运算满足以下八条公理，则称集合 V 是在域 F 上的一个线性空间或向量空间。

八条公理

关于向量加法（要求 (V, +) 构成一个交换群）：

1. 加法结合律 :
   对于任意 u, v, w ∈ V，有 (u + v) + w = u + (v + w)。（解读：加法的顺序不影响结果。）
2. 加法交换律 :
   对于任意 u, v ∈ V，有 u + v = v + u。（解读：谁加谁都一样。）
3. 存在零向量 :
   在 V 中存在一个唯一的元素 0（称为零向量），使得对于任意 v ∈ V，都有 v + 0 = v。（解读：存在一个“什么都不改变”的中性向量。）
4. 存在加法逆元 :
   对于 V 中的每一个向量 v，都存在一个向量 -v（称为 v 的负向量），使得 v + (-v) = 0。（解读：每个向量都有一个可以“抵消”它的伙伴。）

关于标量乘法与向量加法的相互作用：

1. 标量乘法对向量加法的分配律 :
   对于任意标量 k ∈ F 和任意向量 u, v ∈ V，有 k(u + v) = ku + kv。（解读：可以先把向量加起来再缩放，也可以先分别缩放再相加。）
2. 标量乘法对标量加法的分配律:
   对于任意标量 k, m ∈ F 和任意向量 v ∈ V，有 (k + m)v = kv + mv。（解读：可以先把标量加起来再缩放，也可以先分别用标量缩放再把结果向量相加。）
3. 标量乘法与标量乘法定义的相容性:
   对于任意标量 k, m ∈ F 和任意向量 v ∈ V，有 k(mv) = (km)v。（解读：多次缩放可以合并为一次缩放。）
4. 标量乘法的单位元 :
   域 F 中的乘法单位元 1 满足：对于任意向量 v ∈ V，有 1v = v。（解读：用数字 1 去缩放向量，向量保持不变。）

例1：F上的标准线性空间 Fⁿ

1. 域 (Field) F:
   这是我们的标量集合。通常情况下，F 就是实数域 R。但它也可以是复数域 C，有理数域 Q，甚至是有限域（如 {0, 1}）。

2. 集合 (Set) V:
   这里的集合 V 就是 Fⁿ。Fⁿ 的定义是所有包含 n 个元素的有序数组（也称为 n-元组, n-tuples）的集合，其中每个元素都来自于域 F。你可以把它想象成 n 维坐标空间。我们处理二维平面上的点 (x, y) 时，我们实际上是在 R² 空间中工作。类似的我们处理三维空间中的点 (x, y, z) 时，我们就是在 R³ 空间中。Fⁿ 就是将这个概念推广到由任意一个域 F 中的数组成的 n 元有序数组，也可以理解为F上的n次笛卡尔积。
   V = Fⁿ = { (x₁, x₂, ..., xₙ) | xᵢ ∈ F for i = 1, 2, ..., n }=F×F…×F

   • Fⁿ 中的一个向量 v 就是一个有序数组，例如 v = (x₁, x₂, ..., xₙ)。
   • 这些 xᵢ 被称为向量 v 的分量或坐标。

3. 两种运算的定义

   为了使 Fⁿ 成为一个线性空间，我们必须定义向量加法和标量乘法。这里的定义非常直观，都是按分量 (component-wise) 进行的。

   设 u = (u₁, u₂, ..., uₙ) 和 v = (v₁, v₂, ..., vₙ) 是 Fⁿ 中的任意两个向量，k 是域 F 中的任意一个标量。

   • 向量加法 (+):
     u + v = (u₁ + v₁, u₂ + v₂, ..., uₙ + vₙ)
   • 标量乘法 (·):
     kv = (kv₁, kv₂, ..., kvₙ)

4. Fⁿ 是所有有限维线性空间的“样板”。有一个非常重要的结论是：任何一个在域 F 上的 n 维线性空间，都与 Fⁿ 同构（isomorphic）。这意味着从代数结构上看，它们是完全一样的。后续定理2会有相应的证明。

例2：几何空间作为线性空间

1. 域 (Field) F:
   在几何和物理世界中，我们用来“缩放”向量的数是实数。因此，标量域是实数域 F = R。

2. 集合 (Set) V:
   集合 V 是三维空间 E³ 中所有自由向量的集合。

   • 向量是什么？ 一个向量是由长度和方向唯一确定的有向线段。
   • “自由”是什么意思？ 这意味着我们不关心向量的起点。只要两个箭头的长度和方向完全相同，我们就视它们为同一个向量。例如，从点 (0,0,0) 指向 (1,2,3) 的向量，与从点 (5,5,5) 指向 (6,7,8) 的向量是完全相同的。

3. 两种运算的定义

   这里的运算遵循我们在物理学或几何学中学到的直观规则。

   • 向量加法 (+):
     对于两个向量 u 和 v，它们的和 u + v 可以通过以下两种等价的方式得到：
     • 平行四边形法则 (Parallelogram Rule): 将 u 和 v 的起点放在同一点，以这两个向量为邻边作一个平行四边形，那么从起点出发的对角线所代表的向量就是 u + v。
     • 首尾相接法 (Head-to-Tail Rule): 将向量 v 的起点移动到向量 u 的终点，那么从 u 的起点指向 v 的终点的新向量就是 u + v。
       无论哪种方法，两个几何向量相加的结果显然还是一个几何向量，因此加法是封闭的。
   • 标量乘法 (·):
     对于一个标量 k ∈ R 和一个向量 v ∈ E³，它们的积 kv 是一个新的向量，其定义如下：
     • 方向： 如果 k > 0，kv 的方向与 v 相同。如果 k < 0，kv 的方向与 v 相反。如果 k = 0，结果是零向量。
     • 长度： kv 的长度是 v 的长度的 |k| 倍。
       这个过程本质上是在对向量进行拉伸、压缩或反向，结果仍然是一个几何向量，因此标量乘法也是封闭的。

例3：函数空间

1. 域 (Field) F:
   我们考虑的函数通常是输出实数的，因此我们用来缩放它们的标量也自然是实数。所以，标量域是 F = R。
2. 集合 (Set) V:
   集合 V 是定义在某个公共定义域 S 上的所有实值函数的集合。记作 F(S, R)。
   V = F(S, R) = { f | f: S → R }

• 这里的 S 可以是任何集合或区间，但最常见的例子是一个闭区间 [a, b]。
• V 中的一个向量就是一个函数 f。f: S → R 的意思是，集合 V 中的任何一个函数 f，都接受一个来自定义域 S 的输入 x，并产生一个实数作为输出 f(x)。这正是为什么在描述中称其为“所有实值函数”的集合——因为它们的函数值（输出）都是实数。
• 这里的 R 指的是函数的上域 (Codomain)，也就是函数所有可能的输出值所在的集合在实数域中。
• 类似的我们可以定义V = F(S, R²)= { f | f: S → R² }。R² 代表的是二维实数向量空间，也就像是我们通常所说的平面直角坐标系。这个空间中的每一个元素都是一个有序实数对，例如 (x, y)。V 中的一个“向量”是一个二值函数 f。注意不是二元函数，他不是有两个自变量，而是有两个输出的分量。这个函数 f 的输出不再是一个单独的实数，而是一个二维向量。也就是说，对于定义域 S 中的任意一个输入 x，f(x) 的结果是 (y₁, y₂) 这样的一个向量。所以，这个函数 f 实际上可以看作是由两个普通的实值函数组成的，举个例子f(t) = (cos(t), sin(t))。V = F(S, R²) 是所有“向量值函数”（具体来说是输出二维向量的函数）所构成的集合。这个集合在逐点的向量加法和标量乘法下，也构成了一个向量空间。

3. 两种运算的定义

和 Fⁿ 类似，函数空间中的运算也是“逐点 (pointwise)”定义的。这意味着对函数的操作，被转化为对函数在每一个点上的值的操作。

设 f 和 g 是 V 中的任意两个函数（即两个“向量”），k 是 R 中的任意一个标量。

• 向量加法 (函数加法):
  它们的和 f + g 是一个新的函数，这个新函数在任意一点 x ∈ S 的取值被定义为：
  (f + g)(x) = f(x) + g(x)
• 标量乘法 (函数与数的乘法):
  k 与 f 的积 kf 也是一个新的函数，这个新函数在任意一点 x ∈ S 的取值被定义为：
  (kf)(x) = k · f(x)

理解1：线性空间的本质

线性空间的本质是一个完整的代数结构，它由一个非空集合、一个数域（通常是实数）以及定义在该集合上的两种封闭运算（向量加法和标量乘法）共同构成。这个结构之所以被称为“线性空间”，关键在于这两种运算必须严格遵守八条公理，这些公理是针对运算本身的行为准则，确保了它们是和谐且一致的。

这引出了线性代数最核心的抽象思想：集合中的元素可以是任意的——无论是几何箭头、矩阵，还是更为抽象的函数与多项式，其具体形态都无关紧要；相应地，作用于这些元素之上的“加法”和“标量乘法”的具体形式也是根据元素类型而定义的。因此，只要我们为某个集合所定义的运算能够满足全部公理，那么这个集合连同其运算就构成了一个线性空间。

此时，无论该集合的元素原本是什么，我们都可以赋予它们一个统一而强大的名字——“向量”，并用同一套线性代数的理论去分析和研究它们，被称为向量的元素可以是函数也可以是一个真的向量，这无所谓，我们研究对象是满足公理的代数结构，而不是元素的具体形态（如箭头或函数）。

定义3：向量组及向量组拼成的抽象矩阵

设 V 是 F 上的线性空间，V 中的任意有限个向量组成的有序集合，称为一个向量组 。例如，从 V 中取出 m 个向量 α₁, α₂, ..., αₘ，它们就构成了一个向量组。为了方便地研究和操作向量组，我们将其形式上地拼成一个行矩阵，这个矩阵的每一个“元素”就是一个向量。我们称其为抽象矩阵 或“向量的矩阵”。

记作：A = (α₁, α₂, ..., αₘ)

这个 A 看起来像一个 1 × m 的矩阵，但它的特别之处在于，它的成员 αᵢ 不是标量（数字），而是来自线性空间 V 的向量。

定义4：向量组的线性相关性

常规表示

设 V 是数域 F 上的线性空间，有一个向量组 α₁, α₂, ..., αₘ。

如果存在一组不全为零的标量 k₁, k₂, ..., kₘ (其中 kᵢ ∈ F)，使得这个向量组的线性组合等于零向量 0：k₁α₁ + k₂α₂ + ... + kₘαₘ = 0

那么，我们就称这个向量组是线性相关 (Linearly Dependent) 的。

反之，如果只有当 k₁, k₂, ..., kₘ 全部为零时，才能使得上述等式成立，那么我们就称这个向量组是线性无关 (Linearly Independent) 的。

直观含义

• 线性相关（“有关”）： 向量组内部存在“冗余”。至少有一个向量是多余的，因为它可以被其他向量的线性组合来表示。
  • 例如，如果 k₁α₁ + k₂α₂ + k₃α₃ = 0 且 k₁ ≠ 0，我们就可以移项得到：
    α₁ = (-k₂/k₁)α₂ + (-k₃/k₁)α₃
    这清晰地表明 α₁ 完全可以由 α₂ 和 α₃ “拼凑”出来，所以它是冗余的。
• 线性无关（“无关”）： 向量组中没有冗余成员。每一个向量都贡献了一个“新的、独立的方向”。你无法从组里的其他向量中构造出任何一个向量。

矩阵表示

这个定义可以借助我们刚刚定义的抽象矩阵 A = (α₁, α₂, ..., αₘ) 和标量列向量 x = [k₁; k₂; ...; kₘ] 来表述，这使得它与线性方程组理论直接挂钩：

• 向量组 A 是线性相关的 ⇔ 齐次线性方程 Ax = 0 存在非零解 ⇔ 存在一组不全为零[k₁; k₂; ...; kₘ] 使得这个向量组的线性组合等于零向量 0
• 向量组 A 是线性无关的 ⇔ 齐次线性方程 Ax = 0 仅有零解。

定义5：两个向量组之间的线性表示

常规表达

设 V 是数域 F 上的线性空间，并设有两个向量组：

• 向量组 A: α₁, α₂, ..., αₘ
• 向量组 B: β₁, β₂, ..., βₙ

如果向量组 A 中的每一个向量 αᵢ (for i = 1, ..., m) 都可以表示为向量组 B 的一个线性组合，那么我们就称向量组 A 可以由向量组 B 线性表示。

矩阵表达

这个概念同样可以用我们之前引入的抽象矩阵 A = (α₁, ..., αₘ) 和 B = (β₁, ..., βₙ) 来进行表述。

向量组 A 可以由向量组 B 线性表示 ⇔ 矩阵方程BX=A有解（可以是任意解），即存在一个 n × m 的标量矩阵 K，使得：A = BK

定义6：线性表示关系的传递性

文字定义

设 V 是数域 F 上的线性空间，并设有三个向量组：

• 向量组 A: α₁, α₂, ..., αₘ
• 向量组 B: β₁, β₂, ..., βₙ
• 向量组 C: γ₁, γ₂, ..., γₚ

如果向量组 A 可以由向量组 B 线性表示，并且向量组 B 可以由向量组 C 线性表示，那么，向量组 A 一定可以由向量组 C 线性表示。这个性质，就称为线性表示关系的传递性。

使用矩阵证明

已知条件：

1. 向量组 A 可以由向量组 B 线性表示。根据定义5，这等价于存在一个 n × m 的标量矩阵 K₁，使得：A = BK₁
2. 向量组 B 可以由向量组 C 线性表示。同理，这等价于存在一个 p × n 的标量矩阵 K₂，使得：B = CK₂

证明目标：
我们需要证明向量组 A 可以由向量组 C 线性表示。也就是说，我们需要找到一个 p × m 的标量矩阵 K，使得：A = CK

证明过程：
我们将已知的两个等式结合起来。将第二个等式 B = CK₂ 代入第一个等式中 B 的位置：A = (CK₂)K₁

由于矩阵的乘法满足结合律，我们可以重新组合括号：A = C(K₂K₁)

现在，我们观察这个结果。K₂ 是一个 p × n 的标量矩阵，K₁ 是一个 n × m 的标量矩阵。它们二者的乘积 K₂K₁ 是一个 p × m 的矩阵，并且它的所有元素也都是标量。

因此，我们令 K = K₂K₁。这个新矩阵 K 就是我们想要寻找的那个 p × m 的标量矩阵。

理解2：抽象和具体的转换

我们将研究焦点从整个空间缩小到向量组（有限个向量的有序集合）。由此引入了抽象矩阵 A = (α₁, ..., αₘ) 的概念。这是一个关键步骤，其目的就是为了将抽象的向量关系**“翻译”成具体的矩阵方程**，从而利用代数工具进行分析。

在此之前，“线性空间”的概念是高度抽象的，它适用于几何箭头、函数、多项式等万事万物。但这种普适性也带来了困扰：我们如何去“计算”或“证明”这些抽象事物之间的关系？我们的策略是，将这些抽象问题“翻译”成一种我们熟悉且擅长的语言——线性方程组。通过这种方式，我们成功地将关于抽象“向量”的性质判断问题，转化为了关于具体“标量”的方程求解问题。

我们目前还只是小试牛刀，将“向量组”的性质和关系的问题进行了转化。而我们最终的目标，正如那张核心的“交换图”所揭示的，是要将整个线性空间和作用于其上的线性变换，都纳入这个强大的“抽象—具体”转换框架中。为此，我们还需要先理解一下向量组的本质才可以。

定义7：向量组的极大线性无关子组

设 V 是数域 F 上的线性空间，设有一向量组 A: α₁, α₂, ..., αₘ∈V。

如果我们在 A 中选出 r 个向量（r ≤ m）组成一个部分组，记作 A₀，且 A₀ 满足以下两个条件：

1. 线性无关性： 部分组 A₀ 本身是线性无关的。
2. 极大性（生成性）：在 A₀ 中加入 A 中任何一个不属于 A₀ 的向量，得到的新向量组都是线性相关的。 （原向量组 A 中的任意一个向量，都可以由 A₀ 线性表示。）

那么，我们就称 A₀ 是向量组 A 的一个极大线性无关组。母组可由其极大线性无关子组线性表示。

证明：描述中的极大性和生成性是等价的

假设 A₀ = {β₁, β₂, ..., βᵣ} 是一个线性无关的向量组。

(1) 证明：生成性 ⇒ 极大性

假设 :
我们假设 生成性 成立。也就是说，对于 A 中的任意向量 α，都存在一组标量 c₁, ..., cᵣ 使得：
α = c₁β₁ + c₂β₂ + ... + cᵣβᵣ

目标:
我们需要证明 极大性 成立。即，任取一个向量 α ∈ A 且 α ∉ A₀，我们需要证明新的向量组 A₀' = {β₁, β₂, ..., βᵣ, α} 是线性相关的。

证明过程：
根据我们的假设，向量 α 可以被 A₀ 线性表示。所以，存在标量 c₁, ..., cᵣ 使得：α = c₁β₁ + c₂β₂ + ... + cᵣβᵣ

将这个等式移项，我们得到：c₁β₁ + c₂β₂ + ... + cᵣβᵣ - α = 0

现在我们来考察这个等式。这是向量组 A₀' ({β₁, ..., βᵣ, α}) 的一个线性组合，其结果是零向量。由定义4可知，为了证明 A₀' 是线性相关的，我们只需要找到一组不全为零的系数。在这个线性组合中，向量 α 的系数是 -1，它显然不为零。因此，我们找到了一组不全为零的系数 (c₁, c₂, ..., cᵣ, -1)，使得向量组 A₀' 的线性组合为零。

(2) 证明：极大性 ⇒ 生成性

假设 :
我们假设 (2) 极大性 成立。也就是说，对于 A 中任意一个不属于 A₀ 的向量 α，向量组 A₀' = {β₁, β₂, ..., βᵣ, α} 都是线性相关的。

目标
我们需要证明 (1) 生成性 成立。即，对于 A 中的任意向量 α，它都可以被 A₀ 线性表示。

证明过程：
我们任取一个 A 中的向量 α。分两种情况讨论：

• 情况一：α ∈ A₀
  如果 α 本身就在 A₀ 中，那么它显然可以被 A₀ 线性表示。例如，如果 α = βᵢ，那么 α = 0·β₁ + ... + 1·βᵢ + ... + 0·βᵣ。

• 情况二：α ∉ A₀
  这是证明的核心。根据我们的极大性假设，向量组 A₀' = {β₁, β₂, ..., βᵣ, α} 是线性相关的。
  根据线性相关的定义，存在一组不全为零的标量 k₁, k₂, ..., kᵣ, k 使得：
  k₁β₁ + k₂β₂ + ... + kᵣβᵣ + kα = 0

  现在，我们来断言 k 必定不等于零 (k ≠ 0)。

  • 为什么？ 我们可以用反证法。假设 k = 0，那么上面的等式就变成了 k₁β₁ + k₂β₂ + ... + kᵣβᵣ = 0。
  • 但我们已知 A₀ = {β₁, ..., βᵣ} 本身是线性无关的。
  • 对于一个线性无关的向量组，唯一能使其线性组合为零的系数只有全零这一种情况。所以，必然有 k₁ = k₂ = ... = kᵣ = 0。
  • 这样一来，如果 k=0，就会导致所有的系数 (k₁, ..., kᵣ, k) 都等于零。但这与我们“系数不全为零”的前提相矛盾。
  • 因此，我们的假设 k=0 是错误的。所以 k 必定不等于零。

  既然 k ≠ 0，我们就可以把含有 α 的项留在左边，其他项移到右边，然后两边同时除以 k：
  kα = -k₁β₁ - k₂β₂ - ... - kᵣβᵣ
  α = (-k₁/k)β₁ + (-k₂/k)β₂ + ... + (-kᵣ/k)βᵣ

  这个等式清晰地表明，α 是向量组 A₀ 的一个线性组合。

定理1：向量组的极大线性无关子组所含向量的个数是唯一的

设 A 是一个非零向量组。如果在 A 中可以找到两个不同的极大线性无关组，分别记为 A₀ 和 B₀，那么这两个向量组所包含的向量个数必然是相等的。

已知条件:

• 向量组 A₀ = {α₁, ..., αᵣ} 是 A 的一个极大线性无关组。
• 向量组 B₀ = {β₁, ..., βₛ} 是 A 的另一个极大线性无关组。

证明目标: 证明 r = s。我们将通过证明 r ≤ s 和 s ≤ r 来完成。

证明过程

1. 根据 B₀ 是 A 的极大线性无关组的定义，它必须能够线性表示原向量组 A 中的所有向量。这是一个由定义直接保证的强大属性。

   (1) 向量组 A 可以由向量组 B₀ 线性表示。

2. A₀ 是从 A 中选出的一个子集。因此，A₀ 中的每一个向量天然地都属于 A。

   (2) 向量组 A₀ 是向量组 A 的一个子组。

3. 我们将上述两点结合：既然 B₀ 能够线性表示 A 中的每一个向量（由(1)），而 A₀ 的所有向量又都属于 A（由(2)），那么 B₀ 必然也能够线性表示 A₀ 中的每一个向量。

   (3) 因此，向量组 A₀ 可以由向量组 B₀ 线性表示。

4. 一方面，A₀ 本身是一个含有 r 个向量的线性无关组（这是 A₀ 作为极大线性无关组的另一个基本属性）。另一方面，A₀ 可以被一个含有 s 个向量的组 B₀ 线性表示（我们刚刚在(3)中推导出的结论）。

   根据线性代数中的基本定理（替换引理）：一个线性无关的向量组若能被另一个向量组线性表示，则其向量个数不能超过后者的向量个数，直观理解就是低维空间无法表示高维空间，而高维空间可以表示低维空间，被表示的空间的维度一定小于表示空间的维度

   由此，我们直接得出结论：

   (4) r ≤ s

由于 A₀ 和 B₀ 的地位是完全对称的，我们可以完全重复上述推理过程，只需将 A₀ 和 B₀ 的角色互换，即可同样得到 s ≤ r。因为 r ≤ s 和 s ≤ r 必须同时成立，所以唯一可能的结论是 r = s。

注：老师课上给的是另一种证法，我这里是直接套了引理，同时老师课上也给出了另一个引理。扁的齐次线性方程必有非零解，对系数矩阵 K 进行高斯消元。因为矩阵只有 m 行，所以主元（pivots）的个数最多也只有 m 个。但我们有 n 个变量（n 列），并且 n > m，所以必然存在至少 n-m 个没有主元的列。这些列对应的变量就是自由变量。只要我们给任意一个自由变量赋一个非零值（例如1），就必然能解出一组非零的解 x，设为w。BZ=C，则B(Zw)=Cw,则Cw=0,因为C是线性无关的，所以w只能全为0.与之前的结果矛盾。

定义8：向量组的秩

一个向量组 A 的极大线性无关组所包含的向量的个数，称为该向量组 A 的秩。记作 rank(A) 或者 r(A)。

• 零向量组的秩： 只包含零向量的向量组 A = {0, 0, ..., 0}，其秩规定为 0。因为它没有任何一个线性无关的子集（除了空集）。
• 秩与线性相关性的关系：
  • 对于一个包含 m 个向量的向量组 A，rank(A) = m ⇔ 向量组 A 线性无关。
  • rank(A) < m ⇔ 向量组 A 线性相关。
• 秩与线性表示的关系：
  • 如果向量组 A 可以被向量组 B 线性表示，那么 rank(A) ≤ rank(B)。
  • 等价向量组： 如果向量组 A 和 B 可以相互线性表示（称为等价向量组），那么它们的秩必然相等：rank(A) = rank(B)。

理解3：极大线性无关组

这是一个承上启下的定义，引出了下一节，基与坐标的概念。我们使用极大无关组正式定义什么是一个向量组的“最精简的、无冗余的、但又能代表全体”的核心子集，同时我们证明了找到的这个“核心”的规模不是随意的，而是一个向量组内在的、恒定的属性，我们将其命名为秩。

由此，我们可以将一个抽象且庞杂的向量组简化为少数几个独立的向量的组合，只不过当前我们是在有限的向量组中进行的计算，而对于线性空间来说，除了只包含零向量的线性空间外，多数都是含有无限个向量的集合，我们需要进一步的推广。

定义9：基与坐标

基

设 V 是数域 F 上的一个线性空间。

如果存在一个正整数 n，以及 V 中的一个向量组 B = {α₁, α₂, ..., αₙ}，使得：

1. 线性无关性： 向量组 B 是线性无关的。
2. 生成性： V 中的任意一个向量 α，都可以由向量组 B 线性表示。

那么，我们就称 V 是一个 n 维线性空间，而向量组 B 就称为 V 的一组基（坐标系）

称为基矩阵。

如果无法找到一组基向量来表示整个线性空间，我们则称这个空间是一个无限维的线性空间。

坐标

现在，既然 {α₁, α₂, ..., αₙ} 构成了一组基，那么对于空间 V 中的任意一个向量 α，都存在一组标量 k₁, k₂, ..., kₙ，使得：

α = k₁α₁ + k₂α₂ + ... + kₙαₙ

由于基向量是线性无关的，上述线性组合的表示方式是唯一的。

这一组唯一的、有序的标量 (k₁, k₂, ..., kₙ)，就被称为向量 α 沿着该基的坐标向量。

为了方便运算和表示，我们通常将这组坐标写成一个列向量的形式：

于是对于任意一个抽象向量 α 就可以被表示为基矩阵 B 与其坐标向量 x 的乘积。

定理2：基（坐标系）实现了抽象线性空间到标准线性空间的一一对应

定理陈述：
设 V 是数域 𝔽 上的一个 n 维线性空间。一旦在 V 中选定一组基 B，那么通过坐标化建立的、从 V 到 𝔽ⁿ 的映射，是一个一一对应 的关系。

更进一步，这个映射还保持了线性运算的结构（即加法和标量乘法），因此它是一个**同构映射 **。

证明过程：

1. 证明它是“单射” : 不同的向量，坐标必然不同。

• 假设有两个不同的向量 α ≠ β。我们想证明它们的坐标 x 和 y 也必然不同。
• （反证法）假设它们的坐标相同，x = y。这意味着 α 和 β 是由同一组基向量、通过同一组系数线性组合而成的。 p → q 等价于**¬q → ¬p**
• 但线性组合的结果是唯一的，所以这必然导致 α = β。
• 因此，不同的向量，其坐标必然不同。

2. 证明它是“满射” : 任何一个坐标，都有对应的向量。

• 在 𝔽ⁿ 空间中随便拿一个坐标向量 x = [k₁, ..., kₙ]ᵀ。
• 我们是否总能在 V 空间中找到一个向量 α，它的坐标恰好就是 x？
• 当然可以。我们直接用基来构造它：α = k₁α₁ + ... + kₙαₙ。
• 由于 V 是线性空间，这个构造出来的 α 必然属于 V。根据定义，它的坐标就是 x。
• 因此，任何一个合法的坐标，都有其对应的“真身”向量存在于 V 中。

小知识点

1.求解 Ax = β的问题，本质上就是将向量β按照A的列向量组进行线性展开（或称线性表示）的问题。

假设矩阵 A 是一个 m × n 的矩阵，我们可以把它看作是由 n 个列向量 α₁, α₂, ..., αₙ 并排组成的：

其中，每一个 αᵢ 都是一个 m 维的列向量。

向量 x 是一个 n 维的列向量，包含我们要求解的未知数：

根据矩阵-向量乘法的定义，Ax 的结果恰好就是 A 的列向量 αᵢ 以 x 的分量 xᵢ 为系数的一个线性组合：

所以，Ax = β 这个方程，实际上就是在说：

也就是将β按照基向量进行展开。

2.有限维空间的例子

𝔽ₙ[x] = { 次数 < n, 以 𝔽 中元素为系数的多项式 }。这个符号代表的是“数域 𝔽 上，次数严格小于 n 的所有多项式”构成的集合。它的一组标准基是 B = {1, x, x², ..., xⁿ⁻¹}这个空间里的任何一个“向量”（即一个多项式 p(x)）都可以被唯一地写成：

接下来我们证明一下这个基的线性无关性。即

这里的 0不是指数字0，而是指零多项式，即一个对于所有 x 值，其函数值都为0的多项式 p(x) = 0。直观理解就是一条平行于x轴且穿过原点的一条直线

既然这个方程对所有 x 都成立，那么它必然对我们任意选取的 n 个不同的 x 值也成立。为了方便，我们选取 n 个不同的、非零的数 x1, x2, ..., x_n。

我们将这 n 个值逐一代入 p(x) = 0 的方程中，得到一个包含 n 个方程的、关于未知数 c0, c1, ..., cn-1 的齐次线性方程组：

转化为矩阵形式
这个齐次线性方程组可以写成矩阵形式 Ac = 0，其中 c 是我们要求的系数向量，0 是零向量,其中的每一个元素都是0：

识别并应用范德蒙德行列式
我们立刻认出，这个系数矩阵 A 正是一个范德蒙德矩阵。

根据线性代数的基本理论，一个可逆的齐次线性方程组 Ac = 0 只有唯一零解

我们知道范德蒙德行列式的计算公式为：

得出结论
因为我们特意选取了 n 个互不相同的值，所以对于任意 i，都有 xj - xi ≠ 0。
这意味着乘积中的每一项都不为零，因此整个行列式 det(A) 必然不为零。

所以，我们必然得出：

这就完美地证明了向量组 {1, x, x², ..., xⁿ⁻¹} 是线性无关的。

3.无限维线性空间

𝔽[x] = { f | f ∈ ℱ(𝔽, 𝔽), 且 f 可写成多项式 }。这个符号代表的是“数域 𝔽 上，变量为 x 的所有多项式构成的集合”。他是一个无限维的线性空间。

我们假设结论不成立，即假设 𝔽[x] 是一个有限维空间。如果它是有限维的，那么它必然存在一个由有限个多项式构成的基。我们设这个有限的基为 B = {f₁(x), f₂(x), ..., fₙ(x)}。

• 记 dᵢ = ∂(fᵢ): 我们记下基中每一个多项式 fᵢ(x) 的次数。
• 取 d = max{d₁, d₂, ..., dₙ}: 我们从这 n 个多项式的次数中，找到那个最大的次数，并记为 d。

我们来构造一个新的多项式：

• xᵈ⁺¹ ∈ 𝔽[x]: 这个多项式 p(x) 的次数是 d+1，它显然属于 𝔽[x]（所有多项式的集合）。
• 根据基的定义（生成性），如果 B 真的是 𝔽[x] 的基，那么 p(x) 一定可以被 B 中的向量线性表示。

同样使用范德蒙德行列式求解，最后的结果，系数应当全部为0，但是-1明显不为零，所以假设不成立。

4.范德蒙德行列式的应用

我在查找资料的时候还发现了一种范德蒙德行列式的用法。

多项式插值问题： 在数域 𝔽 中，给定 n 个不同的点 (x₁, y₁), (x₂, y₂), ..., (xₙ, yₙ)，我们是否能找到一个唯一的次数小于 n 的多项式 p(x) ∈ 𝔽ₙ[x]，使得这个多项式的图像恰好穿过所有这 n 个点？

“穿过所有这 n 个点”意味着，对于每一个点 (xᵢ, yᵢ)，都必须满足 p(xᵢ) = yᵢ。
我们将 p(x) 的表达式代入，就可以得到 n 个关于未知系数 c₀, c₁, ..., cₙ₋₁ 的线性方程：

这是一个典型的线性方程组。我们可以把它写成我们熟悉的矩阵形式 Ac = y：

观察这个 n × n 的系数矩阵 A，它的每一行都是 1, xᵢ, xᵢ², ... 的形式。这个具有特殊结构的矩阵，正是范德蒙德矩阵。

现在，我们最初的插值问题——“是否存在唯一的多项式？”——就完全转化为了一个线性代数问题：

这个线性方程组是否存在唯一的解 c = [c₀, ..., cₙ₋₁]ᵀ？

根据克莱姆法则或矩阵理论，一个方阵 A 作为系数矩阵的线性方程组 Ac=y 存在唯一解的充要条件是 A 可逆，这又等价于 A 的行列式不为零，即 det(A) ≠ 0。

而范德蒙德矩阵的行列式（即范德蒙德行列式）有一个非常优美的著名公式：

这个公式的含义是，行列式的值等于所有满足 j > i 的 (xⱼ - xᵢ) 项的乘积。

• 什么时候 det(A) 会等于 0 呢？当且仅当连乘积中至少有一项 (xⱼ - xᵢ) 等于 0。
• 这又当且仅当至少存在一对不相等的下标 i 和 j，使得 xᵢ = xⱼ。

但是，我们最初在插值问题中提出的前提就是“给定 n 个不同的点”，这意味着所有的 x₁, x₂, ..., xₙ 都是互不相等的。

因此，只要所有的 xᵢ 互不相同，范德蒙德行列式 det(A) 就永远不为零！

所以，对于任意 n 个 x 坐标互不相同的点，总能找到一个唯一的、次数小于 n 的多项式，精确地穿过这 n 个点。

理解4：坐标化

我们将“极大线性无关组”的思想从有限的向量组推广到整个线性空间，从而引出基 (Basis) 的定义——能够生成整个空间的线性无关组。 “基”的确立，为抽象空间提供了坐标框架。任何一个抽象向量 α 都可以被唯一地表示为基向量的线性组合 α = Bx，其中的系数 x 就是该向量的坐标向量。紧接着证明了从抽象空间 V 到具体坐标空间 Fⁿ 的这种“坐标化”映射，是一个完美的、保持结构的一一对应关系（同构）。

好，到现在为止，我们应当能够理解最开始那张图的一半了，也就是下面的这个过程，通过确定基向量，我们可以将抽象向量通过对基向量进行展开将坐标一一对应到标准线性空间中。接下来，我通过一系列“小知识点”来巩固和应用前面的理论。从线性组合角度重新诠释 Ax = β 的求解。以 Fₙ[x]（有限维多项式空间）为例，利用范德蒙德行列式来具体证明其标准基的线性无关性，并解决多项式插值问题。通过证明 F[x]（所有多项式空间）的无限维性，反向加深对“基”和“维数”概念的理解。

定义10：子空间

设 V 是数域 𝔽 上的一个线性空间，W 是 V 的一个非空子集 (W ⊆ V, W ≠ ∅)。

如果 W 对于 V 中所定义的向量加法和标量乘法这两种运算也是封闭的，那么，我们就称 W 是 V 的一个线性子空间，简称子空间。

• 加法封闭 (Closed under Addition): 对于任意两个向量 u, v ∈ W，它们的和 u + v 也必须属于 W。
• 数乘封闭 (Closed under Scalar Multiplication): 对于任意标量 k ∈ 𝔽 和任意向量 v ∈ W，它们的积 k·v 也必须属于 W。

**注：**子空间本身按照母空间的加法和数乘操作仍然构成一个线性空间。

例4：向量组的生成子空间及子空间的生成组

设 V 是一个线性空间，S = {α₁, α₂, ..., αₘ} 是 V 中的一个任意的、非空的向量组。

由 S 中向量的所有可能的线性组合所构成的集合，称为由 S 生成 (Span) 的子空间，记作 Span(S) 或者 L(S)。

已知 W，若有向量组 S = {α₁, α₂, ..., αₘ}使得 W=Span(S),则称S为W的生成组

生成组提供了一种子空间的表现方式。

例5： A属于 F^m×n 的核与像

对于一个给定的矩阵 A，它属于 F^m×n（表示一个 m 行 n 列，其中元素属于数域 F 的矩阵），我们可以将其看作一个从 n 维空间 Fⁿ 到 m 维空间 F^m 的线性变换。

1. 核 (Kernel)

定义：
矩阵 A 的核，又称为零空间 (Null Space)，通常记作 Ker(A) 或 N(A)。它是在 Fⁿ 中所有使得矩阵乘法结果为零向量的向量 x 的集合。

数学定义如下：Ker(A) = {x ∈ Fⁿ | Ax = 0}​\in F^n

这里的 0 是 F^m 中的零向量。换句话说，矩阵 A 的核是齐次线性方程组 Ax = 0 的所有解向量组成的集合。这个集合是定义域 Fⁿ 的一个子空间。也就是齐次线性方程组Ax = 0 的解空间

2.矩阵的像 (Image)

矩阵 A 的像，又称为列空间 (Column Space) 或值域 (Range)，通常记作 Im(A) 或 R(A)。它是在 F^m 中所有可以通过矩阵 A 与某个向量 x 相乘得到的向量的集合。

数学定义如下：Im(A) = {Ax | x ∈ Fⁿ}​\in F^m

矩阵 A 的像是其列向量所有可能的线性组合所构成的集合，也就是由 A 的列向量所张成的空间。这个集合是陪域 F^m 的一个子空间。

简单来说，像就是矩阵 A 的列向量能够通过变换产生的所有可能的输出向量的集合。

3.观察

上面的定义可能有些不好理解，我们更加直观的感受一下

一个矩阵 A 乘以一个向量 x，可以看作是矩阵 A 的列向量的线性组合。

如果矩阵 ​ A \in F^{m \times n} ，其列向量为 ​ a_1, a_2, \dots, a_n ，并且向量 ​ x \in F^n ，那么它们的乘积可以表示为：

其中，每个列向量 ​ a_i \in F^m 。

这个乘积的结果等于 A 的列向量以 x 的对应分量为系数的线性组合，也就是列向量组张成的空间：

定义11：子空间的交与和

设 ​V 是一个向量空间，并且 ​U 和 ​W 是 ​V 的两个子空间。

1. 子空间的交

​U 与 ​W 的交，记作 ​U \cap W，是所有同时属于 ​U 和 ​W 的向量的集合。

数学定义如下：​U \cap W = \{ \mathbf{v} \in V \mid \mathbf{v} \in U \text{ 并且 } \mathbf{v} \in W \}

重要性质： 两个子空间的交 ​U \cap W 仍然是 ​V 的一个子空间。 事实上，它是同时包含于 ​U 和 ​W 的最大的子空间。

2. 子空间的和

​U 与 ​W 的和，记作 ​U + W，是所有能够表示为一个 ​U 中的向量与一个 ​W 中的向量之和的向量的集合。

数学定义如下：​U + W = \{ \mathbf{u} + \mathbf{w} \mid \mathbf{u} \in U, \mathbf{w} \in W \}

重要性质： 两个子空间的和 ​U + W 仍然是 ​V 的一个子空间。 它是包含 ​U 和 ​W 的最小的子空间。

3.子空间的并

​U 与 ​W 的并未必是子空间。

理解5：子空间

在通过“基”与“坐标”的概念，成功地为整个抽象线性空间 V 搭建起一个可度量的框架之后，我们自然会把目光投向空间的内部结构。一个庞大的线性空间（如所有函数的空间）往往过于复杂，直接研究其整体性质会很困难。因此，一个有效的策略是去考察其中一些更小、更简单且行为良好的子集。子空间，就是我们寻找的这种“行为良好”的子集。

“行为良好”的核心在于封闭性。一个子空间 W 就像一个“自给自足的迷你线性空间”，它完美地继承了母空间 V 的线性结构。你可以在 W 内部进行任意的向量加法和标量乘法，而永远不必担心会“跑出”W 的边界。这使得我们可以将研究整个大空间的复杂问题，分解为研究其内部各个子空间的性质。

定义本身是抽象的，但例4和例5为我们提供了两种最核心、最具体的构造子空间的方法：

1. 从“内部”构建：生成子空间 (Span)
   Span(S) 的概念告诉我们，任何一个向量组 S 都可以像“种子”一样，通过线性组合“生长”出一个子空间。这是从具体向量出发，向上构建抽象结构的视角。它回答了：“给定几个基本元素，它们能构成一个怎样的线性世界？” 这也与我们之前讨论的“基”紧密相连：一个子空间的基，就是能够生成它的最有效率（线性无关）的“种子集合”。
2. 从“外部”观察：核与像 (Kernel & Image)
   当我们引入一个线性映射（或矩阵 A）时，它就像一个“探针”，可以揭示出空间的内在结构。核 (Kernel) 与像 (Image) 是这个探测过程产生的两个最基本的子空间：
   • 核 Ker(A)：位于输入空间 Fⁿ，它告诉我们哪些向量在变换中会“消失”或被“压扁”成零。它描述了映射的信息损失程度。
   • 像 Im(A)：位于输出空间 Fᵐ，它告诉我们经过变换后所有可能到达的地方。它描述了映射的能力范围或“维度”。

这些知识对于后续基的选择和优化有着非常重要的意义，当前我们暂且先记住。

定义12：线性映射与线性变换

1. 线性映射

设 V 和 W 是在同一个域 F 上的两个向量空间。一个从 V 到 W 的函数（或称为映射） ​\mathcal{A}，如果对于 V 中任意的向量 x, y 和域 F 中任意的标量 k，都满足以下两个条件，则称 ​\mathcal{A} 为一个线性映射：

1. 加法保持性:
   ​\mathcal{A}(\mathbf{x} + \mathbf{y}) = \mathcal{A}(\mathbf{x}) + \mathcal{A}(\mathbf{y})
   (两个向量和的像，等于它们各自的像的和)
2. 齐次性 或数乘保持性 :
   ​\mathcal{A}(k\mathbf{x}) = k\mathcal{A}(\mathbf{x})
   (一个向量数乘的像，等于它像的数乘)

这两个条件也可以合并成一个单一的条件：
​\mathcal{A}(k\mathbf{x} + l\mathbf{y}) = k\mathcal{A}(\mathbf{x}) + l\mathcal{A}(\mathbf{y})
其中 x, y 是 V 中的任意向量，k, l 是域 F 中的任意标量。

• V 称为线性映射 ​\mathcal{A} 的定义域 (Domain)。
• W 称为线性映射 ​\mathcal{A} 的陪域 (Codomain)。

核心思想：线性映射是一种保持向量空间结构的映射。它将定义域中的线性组合关系，原封不动地搬到了陪域中。

2. 线性变换

在线性代数中，线性变换通常是线性映射的同义词。然而，在某些上下文中，线性变换有更狭义的用法：

• 广义上：线性变换就是线性映射。
• 狭义上：当一个线性映射的定义域 V 和陪域 W 是同一个向量空间时 (即 ​\mathcal{A}: V \to V)，这个映射常被称为 V 上的一个线性变换。

注：若一个线性映射 ​\mathcal{A}: V \to W 是可逆的 (invertible)，则称 ​\mathcal{A} 为一个线性同构。

如果存在一个从 V 到 W 的线性同构，我们就说向量空间 V 与 W 是同构的，记作 ​V \cong W。

由此我们可以进一步强化前面的定理，一个有限维的线性空间建立标准坐标系之后他和标准线性空间同构。

例6：矩阵与标准线性空间之间的线性映射两种事物的等同性

给定一个域 F 上的 ​m \times n 矩阵 ​A \in F^{m \times n}。通过（向量）右乘运算，可以决定一个从标准线性空间 ​F^n 到 ​F^m 的线性映射。

这个映射记作 ​\mathcal{A}_A，其定义如下：

方向一：从“矩阵”到“线性映射”

给定任何一个 ​m \times n 的矩阵 A，我们都可以定义一个函数 ​\mathcal{A}(\mathbf{x}) = A\mathbf{x}。我们为什么能确定这个函数一定是一个线性映射呢？

因为矩阵乘法本身的性质就满足线性映射的两条法则：

1. 加法保持性:
   对于任意向量 x 和 y，矩阵的分配律告诉我们：
   ​A(\mathbf{x} + \mathbf{y}) = A\mathbf{x} + A\mathbf{y}
   这正好就是线性映射的第一条要求：​\mathcal{A}(\mathbf{x} + \mathbf{y}) = \mathcal{A}(\mathbf{x}) + \mathcal{A}(\mathbf{y})
2. 数乘保持性:
   对于任意向量 x 和标量 k，矩阵乘法的性质告诉我们：
   ​A(k\mathbf{x}) = k(A\mathbf{x})
   这正好就是线性映射的第二条要求：​\mathcal{A}(k\mathbf{x}) = k\mathcal{A}(\mathbf{x})

方向二：从“线性映射”到“矩阵”

这个方向更关键。它说明了任何一个从 ​F^n 到 ​F^m 的线性映射，都必然可以并且是唯一地用一个 ​m \times n 的矩阵来表示。

我们来看看如何“找到”这个矩阵：

1. 基向量：
   在线性代数中，只要我们知道一个线性映射如何变换一组基向量，我们就能知道它如何变换空间中的任何一个向量。对于输入空间 ​F^n，最简单的一组基是标准基：
   ​\mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}, \quad \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix}, \quad \dots, \quad \mathbf{e}_n = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}

2. 表达任意向量：
   ​F^n 中的任意向量 ​\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} 都可以用这组基表示为：
   ​\mathbf{x} = x_1\mathbf{e}_1 + x_2\mathbf{e}_2 + \cdots + x_n\mathbf{e}_n

3. 施加线性映射：
   现在我们对向量 x 施加线性映射 ​\mathcal{A}：
   ​\mathcal{A}(\mathbf{x}) = \mathcal{A}(x_1\mathbf{e}_1 + x_2\mathbf{e}_2 + \cdots + x_n\mathbf{e}_n)

4. 利用线性性质：
   根据线性映射的定义，我们可以把上式拆开：
   ​\mathcal{A}(\mathbf{x}) = \mathcal{A}(x_1\mathbf{e}_1) + \mathcal{A}(x_2\mathbf{e}_2) + \cdots + \mathcal{A}(x_n\mathbf{e}_n)
   ​\mathcal{A}(\mathbf{x}) = x_1\mathcal{A}(\mathbf{e}_1) + x_2\mathcal{A}(\mathbf{e}_2) + \cdots + x_n\mathcal{A}(\mathbf{e}_n)

5. 构造矩阵：
   观察上式！​\mathcal{A}(\mathbf{e}_1), \mathcal{A}(\mathbf{e}_2), \dots 这些都是经过映射后得到的、存在于输出空间 ​F^m 中的具体列向量。
   让我们把这些列向量并排放在一起，组成一个矩阵 A：
   ​A = \begin{bmatrix} \mathcal{A}(\mathbf{e}_1) & \mathcal{A}(\mathbf{e}_2) & \cdots & \mathcal{A}(\mathbf{e}_n) \end{bmatrix}
   （矩阵 A 的第 j 列，就是基向量 ​\mathbf{e}_j 经过映射 ​\mathcal{A} 后的像）

6. 最后：
   现在，我们用这个构造出来的矩阵 A 去乘以向量 x：
   ​A\mathbf{x} = \begin{bmatrix} \mathcal{A}(\mathbf{e}_1) & \cdots & \mathcal{A}(\mathbf{e}_n) \end{bmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} = x_1\mathcal{A}(\mathbf{e}_1) + x_2\mathcal{A}(\mathbf{e}_2) + \cdots + x_n\mathcal{A}(\mathbf{e}_n)

   我们发现，​A\mathbf{x} 的结果与 ​\mathcal{A}(\mathbf{x}) 的结果完全一样！

结论：对于任何一个线性映射 ​\mathcal{A}，我们总能通过观察它对标准基向量的作用，来构造出一个唯一的矩阵 A，使得 ​A\mathbf{x} 的计算结果与 ​\mathcal{A}(\mathbf{x}) 完全等价。

定义13：线性映射的矩阵表示

设 V 和 W 是域 F 上的两个有限维向量空间，其中 ​\dim(V) = n 且 ​\dim(W) = m。
设 ​\mathcal{B} = \{\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n\} 是 V 的一组基 (称为输入基或始基)。
设 ​\mathcal{C} = \{\mathbf{w}_1, \mathbf{w}_2, \dots, \mathbf{w}_m\} 是 W 的一组基 (称为输出基或终基)。
设 ​\mathcal{A}: V \to W 是一个线性映射。

构造方法如下：

1. 将 V 中的每一个基向量 ​\mathbf{v}_j (for j = 1, 2, ..., n) 通过映射 ​\mathcal{A} 进行变换，得到 W 中的向量 ​\mathcal{A}(\mathbf{v}_j)。

2. 由于 ​\mathcal{A}(\mathbf{v}_j) 是 W 中的向量，因此它可以唯一地表示为 W 的基 ​\mathcal{C} 的线性组合：

   \mathcal{A}(\mathbf{v}_j) = a_{1j}\mathbf{w}_1 + a_{2j}\mathbf{w}_2 + \cdots + a_{mj}\mathbf{w}_m = \sum_{i=1}^{m} a_{ij}\mathbf{w}_i

   这些系数 ​a_{1j}, a_{2j}, \dots, a_{mj} 组成了向量 ​\mathcal{A}(\mathbf{v}_j) 在基 ​\mathcal{C} 下的坐标向量：

   [\mathcal{A}(\mathbf{v}_j)]_{\mathcal{C}} = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \end{pmatrix}

3. 我们将这个坐标向量作为矩阵的第 j 列。对所有来自基 ​\mathcal{B} 的向量都执行此操作，并将得到的列向量并排，就构成了一个 ​m \times n 的矩阵。

这个构造出来的矩阵 A 被称为线性映射 ​\mathcal{A} 关于基 ​\mathcal{B} 和基 ​\mathcal{C} 的矩阵表示，记作 ​[\mathcal{A}]_{\mathcal{B}}^{\mathcal{C}}。

定理3：用坐标计算线性映射

设 ​\mathcal{A}: V \to W 是一个线性映射。

• ​V 空间有一组基 ​\mathcal{B} = \{\epsilon_1, \dots, \epsilon_n\}。
• ​W 空间有一组基 ​\mathcal{C} = \{\eta_1, \dots, \eta_m\}。

给定 ​V 中的任意一个向量 ​\mathbf{v}，其在基 ​\mathcal{B} 下的坐标为 ​\mathbf{x}。
那么，它的像 ​\mathcal{A}(\mathbf{v}) 在 ​W 中的基 ​\mathcal{C} 下的坐标为：

其中，A 是线性映射 ​\mathcal{A} 关于基 ​\mathcal{B} 和基 ​\mathcal{C} 的矩阵表示。

证明：

1. 展开任意向量 ​\mathbf{v}

对于 ​V 中的任意向量 ​\mathbf{v}，它可以被输入基 ​\mathcal{B} = \{\mathbf{v}_1, \dots, \mathbf{v}_n\} 唯一地展开。
设其坐标为 ​x_1, x_2, \dots, x_n，即：

我们可以把这个式子写成一种“矩阵乘法”的形式：

2. 对 ​\mathbf{v} 施加线性映射 ​\mathcal{A}

现在，我们计算 ​\mathcal{A}(\mathbf{v})。利用 ​\mathcal{A} 的线性性质：

这也可以写成同样的“矩阵乘法”形式：

3. 代入公式

代入到上面第2步的式子中。

4. 利用结合律重新组合

由于矩阵乘法满足结合律（即使这里的元素是抽象向量，只要结构正确，结合律仍然成立），我们可以改变括号的位置：

例7：矩阵表示的例子

微分算子

问题设定：

• 设 V 是所有次数不超过3的实系数多项式构成的向量空间 (​P_3(\mathbb{R}))。这是一个4维空间。
• 设 W 是所有次数不超过2的实系数多项式构成的向量空间 (​P_2(\mathbb{R}))。这是一个3维空间。
• 设线性映射 ​\mathcal{D}: V \to W 是微分算子，即 ​\mathcal{D}(p(x)) = p'(x)。

目标：
找到这个抽象的微分算子 ​\mathcal{D}，关于V和W的标准基的矩阵表示 ​A。

第一步：确定输入和输出空间的基

1. 输入空间 V 的基：我们选择 ​P_3(\mathbb{R}) 的标准基 ​\mathcal{B}：

   \mathcal{B} = \{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \mathbf{v}_4\} = \{1, x, x^2, x^3\}

2. 输出空间 W 的基：我们选择 ​P_2(\mathbb{R}) 的标准基 ​\mathcal{C}：

   \mathcal{C} = \{\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3\} = \{1, x, x^2\}

第二步：按照定义构造矩阵 ​A = [\mathcal{D}]_{\mathcal{B}}^{\mathcal{C}}

矩阵的第 j 列，是输入基的第 j 个向量的像，在输出基下的坐标。

• 计算第1列 (j=1):

  1. 取输入基的第1个向量: ​\mathbf{v}_1 = 1。
  2. 施加映射: ​\mathcal{D}(\mathbf{v}_1) = \mathcal{D}(1) = \frac{d}{dx}(1) = 0。
  3. 将结果 ​0 用输出基 ​\mathcal{C} 表示: ​0 = \mathbf{0} \cdot \mathbf{w}_1 + \mathbf{0} \cdot \mathbf{w}_2 + \mathbf{0} \cdot \mathbf{w}_3 = 0 \cdot 1 + 0 \cdot x + 0 \cdot x^2。
  4. 得到坐标向量: ​[\mathcal{D}(\mathbf{v}_1)]_{\mathcal{C}} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}。

• 计算第2列 (j=2):

  1. 取输入基的第2个向量: ​\mathbf{v}_2 = x。
  2. 施加映射: ​\mathcal{D}(\mathbf{v}_2) = \mathcal{D}(x) = 1。
  3. 将结果 ​1 用输出基 ​\mathcal{C} 表示: ​1 = \mathbf{1} \cdot \mathbf{w}_1 + \mathbf{0} \cdot \mathbf{w}_2 + \mathbf{0} \cdot \mathbf{w}_3 = 1 \cdot 1 + 0 \cdot x + 0 \cdot x^2。
  4. 得到坐标向量: ​[\mathcal{D}(\mathbf{v}_2)]_{\mathcal{C}} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}。

• 计算第3列 (j=3):

  1. 取输入基的第3个向量: ​\mathbf{v}_3 = x^2。
  2. 施加映射: ​\mathcal{D}(\mathbf{v}_3) = \mathcal{D}(x^2) = 2x。
  3. 将结果 ​2x 用输出基 ​\mathcal{C} 表示: ​2x = \mathbf{0} \cdot \mathbf{w}_1 + \mathbf{2} \cdot \mathbf{w}_2 + \mathbf{0} \cdot \mathbf{w}_3 = 0 \cdot 1 + 2 \cdot x + 0 \cdot x^2。
  4. 得到坐标向量: ​[\mathcal{D}(\mathbf{v}_3)]_{\mathcal{C}} = \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix}。

• 计算第4列 (j=4):

  1. 取输入基的第4个向量: ​\mathbf{v}_4 = x^3。
  2. 施加映射: ​\mathcal{D}(\mathbf{v}_4) = \mathcal{D}(x^3) = 3x^2。
  3. 将结果 ​3x^2 用输出基 ​\mathcal{C} 表示: ​3x^2 = \mathbf{0} \cdot \mathbf{w}_1 + \mathbf{0} \cdot \mathbf{w}_2 + \mathbf{3} \cdot \mathbf{w}_3 = 0 \cdot 1 + 0 \cdot x + 3 \cdot x^2。
  4. 得到坐标向量: ​[\mathcal{D}(\mathbf{v}_4)]_{\mathcal{C}} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix}。

最终，将这些列向量组合起来，就得到了微分算子的矩阵表示：

现在我们来验证这个矩阵。任取一个V中的向量，例如：

方法一 (直接微分):

方法二 (使用矩阵计算):

1. 找到输入向量 ​\mathbf{p}(x) 在基 ​\mathcal{B} 下的坐标：

   [\mathbf{p}]_{\mathcal{B}} = \begin{pmatrix} 4 \\ -2 \\ 5 \\ -1 \end{pmatrix}

2. 用矩阵 A 左乘这个坐标向量：

   [\mathcal{D}(\mathbf{p})]_{\mathcal{C}} = A \cdot [\mathbf{p}]_{\mathcal{B}} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \end{bmatrix} \begin{pmatrix} 4 \\ -2 \\ 5 \\ -1 \end{pmatrix}
   = \begin{pmatrix} (0)(4) + (1)(-2) + (0)(5) + (0)(-1) \\ (0)(4) + (0)(-2) + (2)(5) + (0)(-1) \\ (0)(4) + (0)(-2) + (0)(5) + (3)(-1) \end{pmatrix} = \begin{pmatrix} -2 \\ 10 \\ -3 \end{pmatrix}

3. 将得到的结果坐标，用输出基 ​\mathcal{C} “翻译”回多项式：

   (-2) \cdot \mathbf{w}_1 + (10) \cdot \mathbf{w}_2 + (-3) \cdot \mathbf{w}_3 = -2 \cdot 1 + 10 \cdot x - 3 \cdot x^2 = -2 + 10x - 3x^2

几何空间绕固定轴旋转的矩阵表示

问题设定：

• 考虑三维实数空间 ​V = W = \mathbb{R}^3。
• 线性变换 ​\mathcal{R}_z(\theta) 表示将空间中的任意向量（或点）绕 Z 轴逆时针旋转一个角度 ​\theta。

目标：
找到这个旋转变换关于标准基的矩阵表示 ​R_z(\theta)。

第一步：确定基

我们使用最直观的标准正交基 ​\mathcal{B} = \mathcal{C} = \{\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3\}。

第二步：分析变换对基向量的作用

我们来考察这个旋转变换对每一个基向量做了什么。

• 对 ​\mathbf{e}_3 的作用:
  向量 ​\mathbf{e}_3 恰好就在旋转轴（Z轴）上。因此，无论旋转多少度，它都保持不变。

  \mathcal{R}_z(\theta)(\mathbf{e}_3) = \mathbf{e}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}

  这是矩阵的第3列。

• 对 ​\mathbf{e}_1 的作用:
  向量 ​\mathbf{e}_1 位于 XY 平面上。绕 Z 轴旋转，它仍然会留在 XY 平面上。这是一个经典的二维旋转问题。
  ​\mathbf{e}_1 从 ​(1, 0) 的位置，旋转 ​\theta 角后，它的新坐标是 ​(\cos\theta, \sin\theta)。

  \mathcal{R}_z(\theta)(\mathbf{e}_1) = \begin{pmatrix} \cos\theta \\ \sin\theta \\ 0 \end{pmatrix}

  这是矩阵的第1列。

• 对 ​\mathbf{e}_2 的作用:
  向量 ​\mathbf{e}_2 同样位于 XY 平面上。它从 ​(0, 1) 的位置，旋转 ​\theta 角后，新坐标是 ​(-\sin\theta, \cos\theta)。

  \mathcal{R}_z(\theta)(\mathbf{e}_2) = \begin{pmatrix} -\sin\theta \\ \cos\theta \\ 0 \end{pmatrix}

  这是矩阵的第2列。

第三步：组合成矩阵

将变换后的基向量坐标作为列，我们得到绕 Z 轴旋转的矩阵表示：

同理，可以得到绕 X 轴和 Y 轴旋转的矩阵：

---

镜面反射的矩阵表示

问题设定：

• 考虑三维实数空间 ​V = W = \mathbb{R}^3。
• 线性变换 ​\mathcal{H} 表示将空间中的任意向量关于一个过原点的平面进行镜面反射。
• 该平面由其单位法向量 ​\mathbf{n} = (n_x, n_y, n_z)^T 唯一确定 (其中 ​n_x^2 + n_y^2 + n_z^2 = 1)。

目标：
找到这个反射变换关于标准基的矩阵表示 ​H。

第一步：推导任意向量的反射公式

直接分析标准基向量如何变换比较复杂。我们先找到一个通用的几何公式。
对于任意向量 ​\mathbf{v}，我们可以将其分解为平行于平面的分量 ​\mathbf{v}_{\parallel} 和垂直于平面的分量 ​\mathbf{v}_{\perp}。

• 垂直分量 ​\mathbf{v}_{\perp} 就是 ​\mathbf{v} 在法向量 ​\mathbf{n} 上的投影：​\mathbf{v}_{\perp} = (\mathbf{v} \cdot \mathbf{n})\mathbf{n}。

• 镜面反射的效果是：平行分量不变，垂直分量反向。

• 因此，反射后的向量 ​\mathcal{H}(\mathbf{v}) 为：

  \mathcal{H}(\mathbf{v}) = \mathbf{v}_{\parallel} - \mathbf{v}_{\perp} = (\mathbf{v} - \mathbf{v}_{\perp}) - \mathbf{v}_{\perp} = \mathbf{v} - 2\mathbf{v}_{\perp}
  \mathcal{H}(\mathbf{v}) = \mathbf{v} - 2(\mathbf{v} \cdot \mathbf{n})\mathbf{n}

  这个公式（称为 Householder 变换）对任意向量 ​\mathbf{v} 都成立。

第二步：将公式应用于标准基

现在我们用这个公式来计算标准基向量 ​\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3 的像。

• 对 ​\mathbf{e}_1 = (1, 0, 0)^T 的作用:
  ​\mathbf{e}_1 \cdot \mathbf{n} = (1,0,0) \cdot (n_x, n_y, n_z) = n_x

  \mathcal{H}(\mathbf{e}_1) = \mathbf{e}_1 - 2n_x\mathbf{n} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - 2n_x \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} 1 - 2n_x^2 \\ -2n_xn_y \\ -2n_xn_z \end{pmatrix}

  这是矩阵的第1列。

• 对 ​\mathbf{e}_2 = (0, 1, 0)^T 的作用:
  ​\mathbf{e}_2 \cdot \mathbf{n} = n_y

  \mathcal{H}(\mathbf{e}_2) = \mathbf{e}_2 - 2n_y\mathbf{n} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} - 2n_y \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} -2n_yn_x \\ 1 - 2n_y^2 \\ -2n_yn_z \end{pmatrix}

  这是矩阵的第2列。

• 对 ​\mathbf{e}_3 = (0, 0, 1)^T 的作用:
  ​\mathbf{e}_3 \cdot \mathbf{n} = n_z

  \mathcal{H}(\mathbf{e}_3) = \mathbf{e}_3 - 2n_z\mathbf{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - 2n_z \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} -2n_zn_x \\ -2n_zn_y \\ 1 - 2n_z^2 \end{pmatrix}

  这是矩阵的第3列。

第三步：组合成矩阵

将这三列组合起来，得到反射矩阵：

这个矩阵可以用更紧凑的形式表示为 ​H = I - 2\mathbf{n}\mathbf{n}^T，其中 ​I 是单位矩阵，​\mathbf{n}\mathbf{n}^T 是向量 ​\mathbf{n} 的外积。

例如： 如果反射平面是 XY 平面，那么法向量是 ​\mathbf{n} = (0, 0, 1)^T。代入公式得到：

这个矩阵的作用是保持 x 和 y 坐标不变，将 z 坐标取反，这正是关于 XY 平面反射的直观效果。

理解6：线性映射的矩阵表示

至此我们完成了对于最开始图像的理解。我们现在有了两条等价的路径。

**路径一：**直接进行抽象运算，比如旋转，镜像。

**路径二：**先坐标化，后具体计算

1. 首先，为输入向量 ​\mathbf{v} 找到它在输入基 ​\mathcal{B} 下的坐标，得到列向量 ​[\mathbf{v}]_{\mathcal{B}}。
2. 然后，用一个特定的 ​m \times n 矩阵 ​A 左乘这个坐标向量，进行一次矩阵乘法，得到结果 ​A \cdot [\mathbf{v}]_{\mathcal{B}}。
3. 最后将坐标转换为向量。

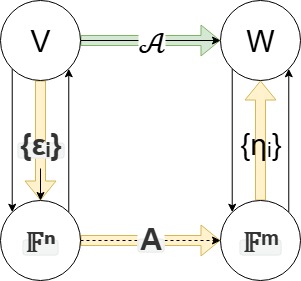
这是一套研究矩阵的思想和技巧，让我们用它来对已经学过的知识做进一步的理解。

定义14：矩阵等价 (Matrix Equivalence)

设 A 和 B 是两个 m x n 矩阵。如果存在 m 阶可逆矩阵 Q 和 n 阶可逆矩阵 P，使得以下关系成立，则称矩阵 A 与 B 是等价的。

1. 代数定义：初等变换形式

矩阵等价的标准定义形式为：

B = QAP

这个表示形式清晰地刻画了通过初等变换从矩阵 A 得到矩阵 B 的过程：

• 左乘 Q: 相当于对矩阵 A 进行一系列的初等行变换。
• 右乘 P: 相当于对矩阵 A 进行一系列的初等列变换。

因此，这个定义在代数上的核心思想是：如果一个矩阵可以通过另一个矩阵经过有限次的初等行列变换得到，那么这两个矩阵就是等价的。

2. 几何定义：基变换形式

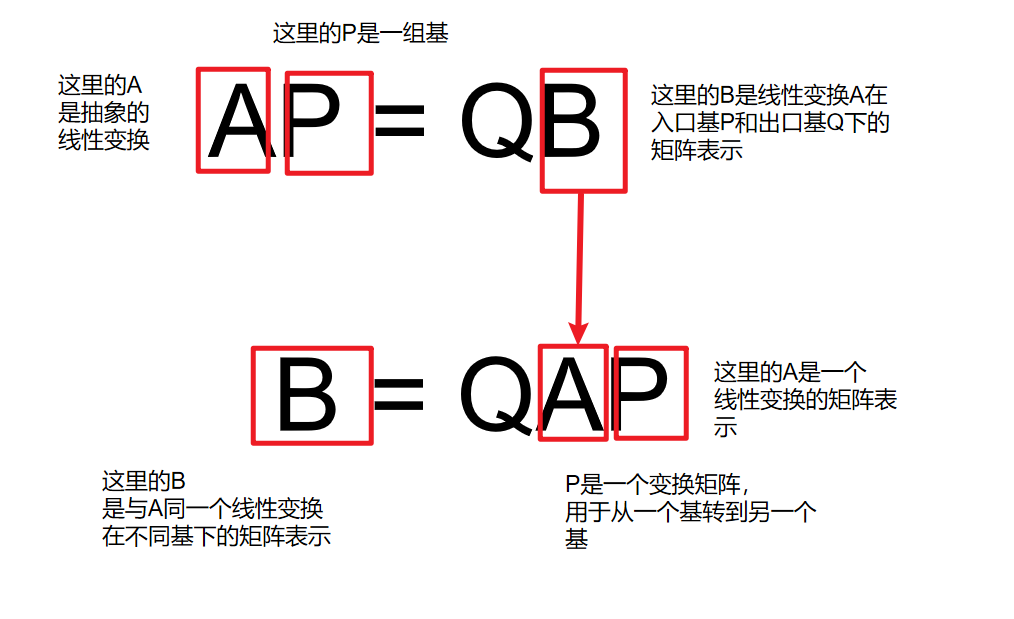
矩阵等价的另一种定义方式是：

AP = QB

这种形式可以从线性映射和空间基变换的角度来理解：

• A 是一个从 n 维线性空间 V (入口) 到 m 维线性空间 W (出口) 的线性映射。
• 可逆矩阵 P 的列向量 [p₁, p₂, ..., pₙ] 构成了 n 维入口空间 V 的一组基。
• 可逆矩阵 Q 的列向量 [q₁, q₂, ..., qₘ] 构成了 m 维出口空间 W 的一组基。

在这个几何框架下，等式 AP = QB 的含义是：
矩阵 B 是线性映射 A 在“入口基 P”和“出口基 Q”下的矩阵表示，直观理解​\mathcal{A}(P) = QB。不知道你们是否还记得例子：微分算子，他最后表示出来的矩阵就是B，微分操作本身就是A，前后是两个不同的空间。

这是一种抽象的思考方式，同样的我们还有一种具体的思考方式。

B = QAP

该等式精确描述了一个复合变换过程，其核心是在特定坐标系下表达同一个线性映射。

设存在一个抽象的线性映射 T，它将 n 维空间 V 中的向量 v 映射到 m 维空间 W 中的向量 w。

• A 是映射 T 在 V 和 W 的旧基下的矩阵表示。
• P 是 V 空间中从新基到旧基的基变换矩阵。其作用是将一个用新基表达的坐标向量，转换为用标准基表达的坐标向量。
• Q 是 W 空间中从旧基到新基的基变换矩阵。其作用是将一个用标准基表达的坐标向量，转换为用新基表达的坐标向量。
• B 是映射 T 在 V 和 W 的新基下的矩阵表示。

B = QAP 这个等式，从右至左，为一个以“新基坐标”为起点的向量，规划了一条通往以“新基坐标”为终点的运算路径：

1. P (坐标正向变换):
   接收一个向量在新输入基下的坐标，将其转换为该向量在旧基下的坐标。这是进入“标准世界”的入口。
2. A (标准空间映射):
   在统一的、通用的旧基体系下，执行核心的线性映射 T。其输出结果是像向量在旧输出基下的坐标。
3. Q (坐标逆向变换):
   接收映射结果在旧输出基下的坐标，将其转换为该结果在新输出基下的坐标。这是从“标准世界”回到“新世界”的出口。

问题1：选择基寻找最简表示

还记得前面我们讨论的子空间的知识点吗，现在需要用到他们了。

目标：最简矩阵表示（标准形）

对于一个秩 (rank) 为 r 的 m x n 矩阵 A，其最简的等价矩阵 B 是一个分块矩阵，形式如下：

B = [ Iᵣ | 0 ]
[ 0 | 0 ]

其中：

• Iᵣ 是 r x r 的单位矩阵。
• 0 代表全零矩阵块。
• 整个矩阵 B 的尺寸仍然是 m x n。

策略：从核与像入手构造基

这里的核心思想是利用线性映射 A 的两个基本子空间：

1. 核 (Kernel or Null Space): 入口空间中所有被 A 映射为零向量的向量集合。
2. 像 (Image or Column Space): 出口空间中所有可以由 A 映射得到的向量集合。

根据秩-零度定理 (Rank-Nullity Theorem)，我们知道：
dim(入口空间) = dim(核) + dim(像)
n = dim(Ker(A)) + rank(A)

这给了我们构造入口基 P 的完美思路。

构造步骤

假设矩阵 A 的秩为 r。

1. 构造入口空间 V 的基 P (n x n 矩阵)

1. 找到核的基：首先，找到 A 的核 Ker(A) 的一组基。因为 rank(A) = r，所以核的维度是 n - r。我们将这 n - r 个基向量命名为 ​{p_{r+1}, p_{r+2}, ..., p_n}。

   • 选择这些向量作为我们新基的一部分，是因为它们经过映射 A 后的结果是零，这显然非常简单。

2. 扩充为完整基：将上面核的基扩充为整个 n 维入口空间 V 的一组基。也就是说，我们再寻找 r 个线性无关的向量 {p₁, p₂, ..., pᵣ}，使得集合 {p₁, ..., pᵣ, p_{r+1}, ..., pₙ} 构成 V 的一组基。

   • 这 r 个向量 {p₁, ..., pᵣ} 就构成了核空间的一个补空间的基。

3. 组成矩阵 P：将这 n 个基向量按顺序作为列，组成可逆矩阵 P：
   ​P = [p₁ | p₂ | ... | pᵣ | p_{r+1} | ... | pₙ]

2. 构造出口空间 W 的基 Q (m x m 矩阵)

我们的目标是让新矩阵 B 的列向量尽可能简单。B 的第 j 列是 Apⱼ 在基 Q 下的坐标。

1. 定义像的基：我们取入口基 P 的前 r 个向量，并用 A 对它们进行映射，得到 r 个向量：{Ap₁, Ap₂, ..., Apᵣ}。可以证明，这 r 个向量线性无关，并且它们构成了 A 的像空间 Im(A) 的一组基。我们将它们定义为出口新基 Q 的前 r 个向量：
   qᵢ = Apᵢ (for i = 1, 2, ..., r)
2. 扩充为完整基：像空间的维度是 r，而整个出口空间 W 的维度是 m。我们再寻找 m - r 个向量 ​{q_{r+1}, ..., qₘ}，使得集合 ​{q₁, ..., qᵣ, q_{r+1}, ..., qₘ} 构成整个 W 的一组基。
3. 组成矩阵 Q：将这 m 个基向量按顺序作为列，组成可逆矩阵 Q：
   ​Q = [q₁ | q₂ | ... | qᵣ | q_{r+1} | ... | qₘ]

验证结果：为什么 B 是标准形？

现在，我们来计算在基 P 和基 Q 下，A 的新矩阵表示 B。根据定义，B 的第 j 列是向量 Apⱼ 在基 Q 下的坐标。

• 对于 j = 1, 2, ..., r:
  我们计算 Apⱼ。根据我们对 Q 的构造，我们有 Apⱼ = qⱼ。
  那么，向量 qⱼ 在基 {q₁, q₂, ..., qₘ} 下的坐标是什么？显然是 (0, ..., 1, ..., 0)，其中 1 在第 j 个位置。这就是标准基向量 eⱼ。
  所以，B 的前 r 列就是 e₁, e₂, ..., eᵣ。
• 对于 j = r+1, ..., n:
  我们计算 Apⱼ。根据我们对 P 的构造，向量 pⱼ (当 j > r) 是 A 的核中的一个基向量。因此，Apⱼ = 0 (零向量)。
  那么，零向量在任何基下的坐标都是 (0, 0, ..., 0)。
  所以，B 的后 n - r 列全是零向量。

把它们组合起来，矩阵 B 就是：

B = [ e₁ | e₂ | ... | eᵣ | 0 | ... | 0 ]

这恰好就是我们期望的标准形矩阵：

B = [ Iᵣ | 0 ]
[ 0 | 0 ]

从几何定义 AP = QB 理解标准形的好处

基础关系

AP = QB 的核心是描述同一个线性映射在不同基下的表示。其第 j 列的等式关系为：
A * pⱼ = Q * bⱼ

这个等式说明：

• 取第 j 个新输入基向量 pⱼ。
• 将其通过原矩阵 A 进行映射，得到向量 A * pⱼ (该向量坐标在旧的标准基下)。
• 这个结果向量 A * pⱼ 等于用新输出基 Q 的列向量，按照 B 的第 j 列 bⱼ 提供的坐标进行线性组合。

简言之，bⱼ 是 A*pⱼ 在基 Q 下的坐标。我们的目标是通过选择 P 和 Q，让 bⱼ 尽可能简单，即让 B 成为标准形。

分析标准形 B 带来的约束和好处

当 B 为标准形 [Iᵣ, 0; 0, 0] 时，我们来看它对基 P 和 Q 施加了什么具体约束，以及这些约束为何是有益的。

1. 对于 j = 1, ..., r (对应 Iᵣ 部分)

• 约束：此时 B 的第 j 列 bⱼ 是标准基向量 eⱼ (第 j 个元素为1，其余为0)。
  代入列等式： A * pⱼ = Q * eⱼ
Q * eⱼ 的结果就是矩阵 Q 的第 j 列 qⱼ。
  因此，等式变为： A * pⱼ = qⱼ
• 解释：这个等式强制要求我们这样选择基：前 r 个新输出基向量 qⱼ，必须是前 r 个新输入基向量 pⱼ 经过映射 A 作用后的像。
• 好处 (解耦)：通过施加这个约束，我们让映射的核心行为变得极其清晰。p₁ 的像就是 q₁，p₂ 的像就是 q₂，...，pᵣ 的像就是 qᵣ。在新坐标系下，从第 j 个输入维度 (pⱼ 方向) 到第 j 个输出维度 (qⱼ 方向) 的映射是直接的、一对一的。所有在原矩阵 A 中存在的复杂交叉影响（耦合）都被消除了，因为这种影响已经被我们选择的基给“吸收”了。

2. 对于 j = r+1, ..., n (对应零矩阵部分)

• 约束：此时 B 的第 j 列 bⱼ 是零向量。
  代入列等式： A * pⱼ = Q * 0
  因此，等式变为： A * pⱼ = 0
• 解释：这个等式强制要求我们这样选择基：后 n-r 个新输入基向量 pⱼ 必须来自矩阵 A 的核 (Kernel / Null Space)。
• 好处 (隔离无效维度)：这个约束将所有对输出没有贡献的输入维度清晰地分离开来。在新坐标系下，任何在这些维度 (​p_{r+1} 到 pₙ 方向) 上的输入分量，其对输出的贡献都直接为零。这使得分析映射的行为时，可以完全忽略这部分输入空间。

从 AP = QB 的角度看，追求标准形 B 的好处是：

• 它不是一个任意的目标，而是迫使我们去寻找能够“对齐”线性映射内在结构的基。
• 这个“对齐”的过程，具体就是让新基的选取与 A 的像空间和核空间这两个基本子空间完全匹配。
• 最终得到的标准形 B，是对这种“对齐”的代数确认。它以最精炼的方式表明：该线性映射在结构上等同于一个 r维的恒等映射和一个 n-r维的零映射的组合。所有复杂的耦合效应都被基变换所处理，使得映射的本质得以揭示,即湮灭其核空间，同时将一个补空间同构地（一一对应且保持结构地）映射到其像空间。

定义15：矩阵的相似

设 A 和 B 都是 n x n 的方阵。如果存在一个 n 阶可逆矩阵 P，使得以下关系成立，则称矩阵 A 与 B 是相似的。

B = P⁻¹AP

这个关系式也可以等价地写为：

PB = AP

核心解读

1. 适用范围：矩阵相似是一个专属于方阵的概念。只有尺寸相同的方阵之间才能讨论相似关系。

2. 变换：与矩阵等价涉及两个不同的可逆矩阵 (P 和 Q) 不同，矩阵相似只涉及一个可逆矩阵 P 和它的逆 P⁻¹。

3. 不变性：相似变换保持了比等价变换多得多的矩阵内在性质。如果两个矩阵 A 和 B 相似，它们必然拥有相同的：

   • 秩 (Rank)
   • 行列式 (Determinant)
   • 迹 (Trace)
   • 特征值 (Eigenvalues)
   • 特征多项式 (Characteristic Polynomial)
   • 最小多项式 (Minimal Polynomial)

几何意义：

矩阵相似那么矩阵一定等价，所以矩阵等价的几何意义同样可以套到矩阵相似中来，但稍微有点区别。矩阵 B 是线性变换 A 在“入口基 P”和“出口基 P”下的矩阵表示.不知道你们是否还记得例子几何空间绕固定轴旋转的矩阵表示，他最后表示出来的矩阵就是B，旋转的操作本身就是A，前后空间相同。

同时，我们还有一种理解：

• 一个空间，一个变换：我们考虑一个 n 维线性空间 V，以及一个从 V 到 其自身 的线性变换 (或称线性算子) T: V → V。
• 矩阵 A 的角色：假设矩阵 A 是这个线性变换 T 在某一组“旧基”（比如标准基）下的矩阵表示。
• 矩阵 P 的角色：矩阵 P 本身是“新基到旧基”的过渡矩阵 (Change-of-Basis Matrix)。相应地，P⁻¹ 是“旧基到新基”的过渡矩阵。
• 矩阵 B 的角色：在这种设定下，矩阵 B 就是同一个线性变换 T，在这组“新基”下的矩阵表示。

公式 B = P⁻¹AP 精确地描述了这种基变换关系：对于一个向量 x，先用 P 从新基坐标转换到旧基坐标，然后应用旧基下的变换 A，最后用 P⁻¹ 将结果从旧基坐标转换回新基坐标，整个过程就等同于直接在新基下应用变换 Bx。下面这张图片来自如何通俗地理解相似矩阵-CSDN博客

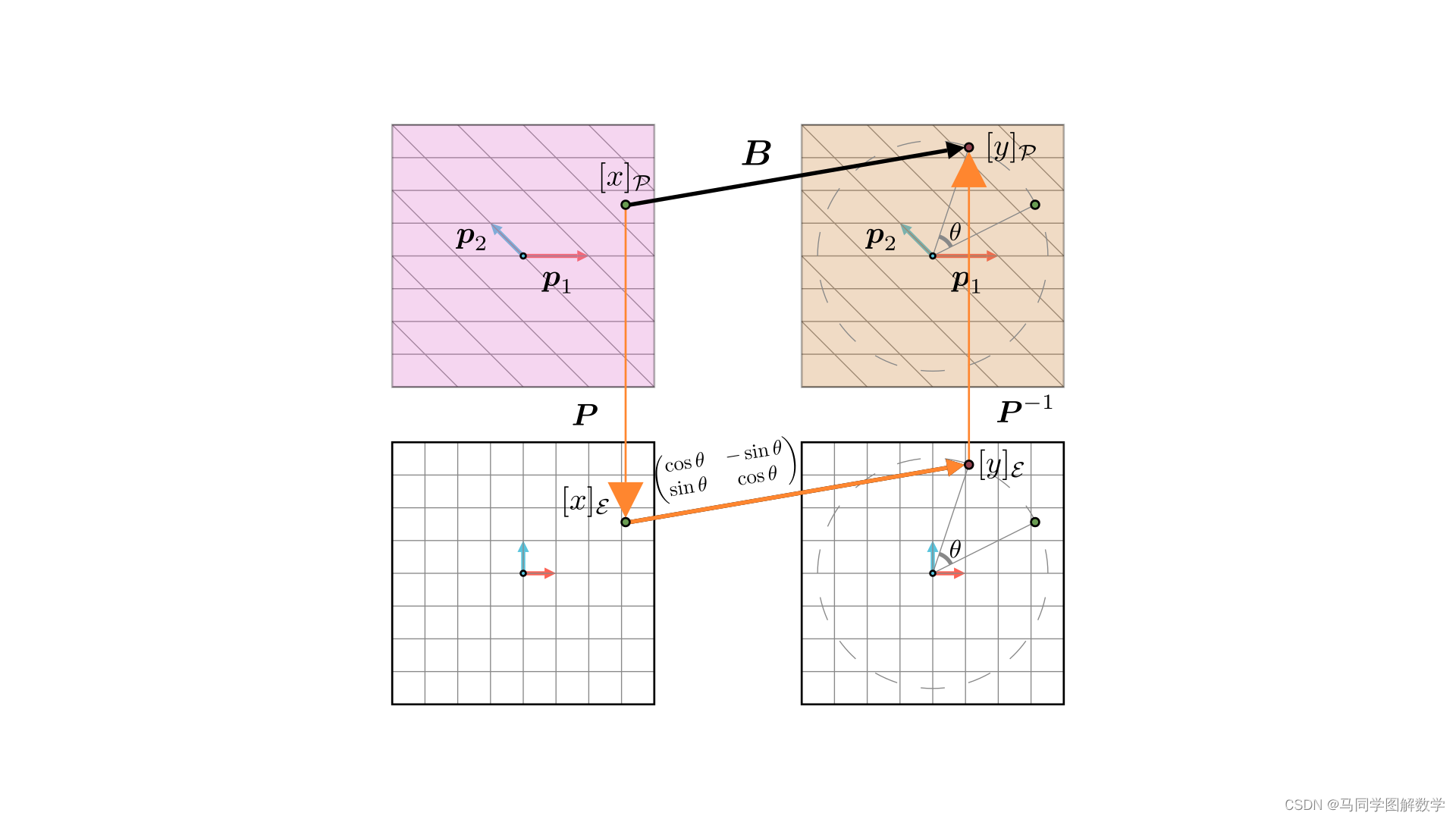
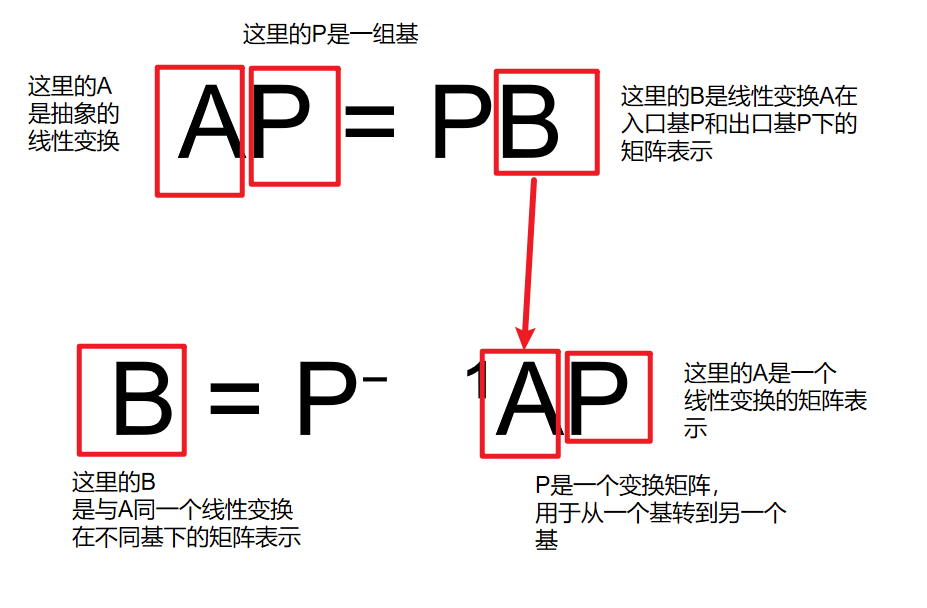
可能有点抽象，大概讲解一下，第一步是将抽象的线性变换变为具体的矩阵，第二步是矩阵间的相互转换，或许第一步写为**​\mathcal{A}(P) = PB`**会更好理解一点，奥，还有一点，为了上下两个图对照起来，我们将第一行的P视为标准正交基，第二行的P视为一般基向标准正交基的变换矩阵。

相似与等价的关键区别

特征	矩阵等价 (Equivalence)	矩阵相似 (Similarity)
定义	AP = QB	PB = AP
矩阵类型	任意 m x n 矩阵	必须是 n x n 方阵
变换矩阵	两个独立的可逆矩阵 P, Q	一个可逆矩阵 P 及其逆 P⁻¹
几何解释	同一个线性映射 (A: V→W)，在两个空间（入口和出口）各自改变基底后的表示	同一个线性变换 (A: V→V)，在一个空间内改变基底后的表示
关系强度	较弱的关系	更强的关系（相似必等价，反之不然）
核心不变量	秩 (Rank)	特征值 (Eigenvalues)、行列式、迹等

定义16：方阵的不变子空间

设 A 是一个 n x n 的方阵，它代表了一个从 n 维线性空间 V 到其自身的线性变换 T: V → V。如果 V 的一个子空间 W 满足以下条件，则称 W 是由 A (或变换 T) 确定的不变子空间：

对于 W 中的任意一个向量 x，其经过矩阵 A 变换后的像 Ax 仍然落在 W 空间内。

用数学语言表述为：

如果 W 是 V 的子空间，且对任意 x ∈ W，都有 Ax ∈ W，则 W 是 A 的一个不变子空间。

为什么不变子空间如此重要？

寻找不变子空间是简化和理解一个线性变换的关键策略。如果我们能将整个空间 V 分解为一系列不变子空间的“直和”（即每个向量都能唯一地表示为来自这些子空间的向量之和），那么我们就可以在每个子空间上独立地研究这个变换。

这对应到矩阵上，就是矩阵的对角化或块对角化。如果找到了合适的不变子空间基，我们就可以通过基变换（相似变换 P⁻¹AP）将复杂的矩阵 A 变成一个更简单的（块）对角矩阵 B。在新的基下，变换的结构一目了然。

基本且重要的不变子空间示例

对于任意一个 n x n 矩阵 A，总存在一些“平庸”或“天然”的不变子空间：

1. 零空间 {0}: 只包含零向量的子空间。因为 A * 0 = 0，结果仍然在 {0} 空间内，所以它总是不变子空间。
2. 整个空间 V: 整个 n 维空间 V 本身。因为 A 的映射目的地就是 V，所以 V 对 A 来说总是不变子空间。

除了这两个，更有意义和启发性的不变子空间包括：

3. 核 (Kernel / Null Space): Ker(A) = {x | Ax = 0}

   • 为什么不变?: 取任意 x ∈ Ker(A)，根据定义 Ax = 0。而零向量 0 必定属于 Ker(A)，所以 Ax 仍然在 Ker(A) 内。因此，核空间是 A 的一个不变子空间。

4. 像 (Image / Column Space): Im(A) = {Ax | x ∈ V}

   • 为什么不变?: 为了证明像空间 Im(A) 是矩阵 A 的一个不变子空间，我们只需说明对于 Im(A) 中的任意向量 y，其像 Ay 依然落在 Im(A) 内部。根据定义，如果 y 属于 Im(A)，那么它必然可以被写作 y = Ax 的形式，其中 x 是定义域 V 中的某个向量。当我们对 y 进行变换时，我们得到 Ay = A(Ax)。这里的关键在于，A是一个自同态映射，将V->V,对于任意 x ∈ V，其像 Ax 必然也是 V 中的一个向量,即Ax∈V。令 z = Ax，A(Ax)= Az 这个表达式完全符合像空间成员的定义——即它是矩阵 A 作用于 V 中某个向量（这个向量恰好是 Ax）的结果。这就证明了 Ay 必然属于 Im(A)，故像空间 Im(A) 对于变换 A 是封闭的，是一个不变子空间。

5. 特征子空间 (Eigenspace):

   • 这是最重要的一类不变子空间。对于 A 的任意一个特征值 λ，其对应的特征子空间 E(λ) = {x | Ax = λx} 是所有对应于 λ 的特征向量以及零向量构成的集合。
   • 为什么不变?: 取 E(λ) 中任意一个向量 x，我们有 Ax = λx。由于 E(λ) 是一个子空间，所以它对数乘封闭，λx 必然也属于 E(λ)。因此，Ax 仍然在 E(λ) 内。
   • 特殊性: 特征子空间不仅是不变的，而且变换在其中的作用极其简单——仅仅是在该向量方向上的拉伸或压缩（乘以因子 λ）。这使得一维的特征子空间（由单个特征向量张成）成为最简单、最理想的不变子空间。

定理4：不变子空间与相似三角化

相似三角化 (Similar Triangularization)： 对于一个方阵 ​A，如果存在一个可逆矩阵 ​P，使得 ​P^{-1}AP 是一个上三角矩阵 ​T，则称 ​A 可以相似三角化。在线性变换的视角下，这意味着存在一组基，使得 ​T 在这组基下的矩阵表示为上三角矩阵。

1. 必要性：相似三角化 ​\implies 存在不变子空间链

假设 ​T 在某组基 ​B = \{v_1, v_2, \dots, v_n\} 下的矩阵 ​A 是一个上三角矩阵。

• 我们构造子空间链 ​W_i = \text{span}\{v_1, v_2, \dots, v_i\}，其中 ​i = 1, 2, \dots, n。
• 显然，这个链满足 ​\{0\} = W_0 \subset W_1 \subset \dots \subset W_n = V 和 ​\dim(W_i) = i。
• 由于 ​A 是上三角矩阵，这意味着对于任意 ​v_j（其中 ​j \le i），​T(v_j) 是 ​v_1, v_2, \dots, v_j 的线性组合。
• 因此， ​T(v_j) \in W_i。由于 ​W_i 由 ​v_1, \dots, v_i 线性张成， ​W_i 中任意向量经 ​T 变换后，结果仍然是 ​v_1, \dots, v_i 的线性组合，即 ​T(W_i) \subseteq W_i。
• 结论： ​W_i 都是 ​T 的不变子空间，不变子空间链存在。

2. 充分性：存在不变子空间链 ​\implies 相似三角化

假设存在不变子空间链 ​\{0\} = W_0 \subset W_1 \subset \dots \subset W_n = V，且 ​\dim(W_i) = i。

• 我们构造一组基 ​B = \{v_1, v_2, \dots, v_n\}，这组基被称为与子空间链相容的基。
• 从 ​W_1 中选取非零向量 ​v_1 作为基向量。
• 由于 ​W_1 \subset W_2，我们将 ​\{v_1\} 扩充为 ​W_2 的基 ​\{v_1, v_2\}。
• 依次类推，将 ​\{v_1, \dots, v_{i-1}\} 扩充为 ​W_i 的基 ​\{v_1, \dots, v_i\}。最终得到 ​V 的一组基 ​B = \{v_1, \dots, v_n\}。
• 现在考察 ​T 在这组基下的矩阵。对于任意 ​v_j，由于 ​v_j \in W_j 且 ​W_j 是不变子空间，所以 ​T(v_j) \in W_j。
• 因为 ​W_j = \text{span}\{v_1, \dots, v_j\}，所以 ​T(v_j) 只能表示成 ​v_1, \dots, v_j 的线性组合。

• 当我们将 ​T(v_j) 的坐标 ​ (a_{1j}, \dots, a_{jj}, 0, \dots, 0)^T 写在矩阵的第 ​j 列时，所有低于主对角线的元素（即 ​a_{k j}，其中 ​k > j）都为零。
• 结论： ​T 在这组基下的矩阵表示为一个上三角矩阵，即 ​T 能够相似三角化。

上面的证明可以取一个特定的值，然后就可以将矩阵分块，变成对角化矩阵，就像老师课上讲的一样。上面的证明结果是不断切分得到的最严格的上三角矩阵。

B = [ A | B ]
[ 0 | C ]

问题2：已有不变子空间。P1，如何找P2构成可逆矩阵

情景设定：

• 我们有一个n维线性空间 V (比如 ​\mathbb{R}^n) 和一个线性变换 T (由n阶方阵A表示)。
• 我们找到了 T 的一个 k维不变子空间 W。
• 我们已经找到了 W 的一组基，由k个线性无关的向量构成：​\{v_1, v_2, \dots, v_k\}。
• 我们将这些基向量作为列，构成了矩阵 P1 = ​[v_1 | v_2 | \dots | v_k]。这是一个 n x k 的矩阵。

目标：

我们的目标是找到另外 n-k 个向量 ​\{v_{k+1}, \dots, v_n\}，将它们构成矩阵 P2 = ​[v_{k+1} | \dots | v_n]，使得由 P1 和 P2 拼接而成的大矩阵 P = [P1 | P2] 是一个n阶可逆矩阵。

P可逆的充要条件是它的所有列向量 ​\{v_1, \dots, v_k, v_{k+1}, \dots, v_n\} 共同构成整个空间V的一组基。

核心任务： 将已知的一组线性无关向量（W的基）扩充为整个空间的基。这个过程在数学上称为基的扩充 (Basis Extension)。

---

如何寻找P2：具体方法

这里提供两种在实践中最常用的方法。

方法一：利用标准基进行筛选（最常用）

这个方法既直观又容易计算，其基本思想是：从整个空间最简单的基（标准基）中，“补充”那些P1的基向量所“缺少”的维度方向。

步骤：

1. 构造增广矩阵：将 P1 的列向量与n维空间中的标准单位向量 ​e_1, e_2, \dots, e_n 并排放在一起，形成一个 n x (k+n) 的大矩阵 M。

   ​M = [v_1 | \dots | v_k | e_1 | e_2 | \dots | e_n]

   （其中 ​e_1 = (1, 0, \dots, 0)^T, ​e_2 = (0, 1, \dots, 0)^T 等）

2. 进行行化简：对矩阵 M 进行行化简（高斯-若尔当消元法），将其化为行最简阶梯形矩阵 (RREF)。

3. 确定主元列：在化简后的RREF矩阵中，找到**主元（pivot）**所在的位置。主元是每行第一个非零元素。

4. 选择基向量：主元所在的列，其在原始矩阵M中对应的列向量，就构成整个空间V的一组基。

   • 由于 ​v_1, \dots, v_k 本身是线性无关的，所以化简后，前k列必定都是主元列。
   • 我们只需要在后面的 ​e_1, \dots, e_n 中，找到另外 n-k 个能够产生新主元列的向量。

5. 构成P2：将这些从 ​\{e_1, \dots, e_n\} 中选出的 n-k 个向量，按顺序排列，就构成了 P2。

示例：

• 设空间为 ​\mathbb{R}^4，不变子空间 W 是由 ​v_1 = (1, 0, 1, 0)^T 和 ​v_2 = (0, 1, 0, 1)^T 张成的。

• 此时 P1 = ​\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{pmatrix}。

• 步骤1： 构造 ​M = [v_1 | v_2 | e_1 | e_2 | e_3 | e_4]

  ​M = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \end{pmatrix}

• 步骤2 & 3： 对 M 进行 RREF 化简：

  ​RREF(M) = \begin{pmatrix} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 0 & -1 \end{pmatrix}

  主元在第1, 2, 3, 4列。

• 步骤4： 这说明原始矩阵M的第1, 2, 3, 4列向量 ​\{v_1, v_2, e_1, e_2\} 构成 ​\mathbb{R}^4 的一组基。

• 步骤5： 我们可以选择 ​v_3 = e_1 和 ​v_4 = e_2 来构成P2。

  P2 = ​[e_1 | e_2] = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \end{pmatrix}

  最终的可逆矩阵 P = [P1 | P2] = ​\begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix}。

方法二：施密特正交化 (Gram-Schmidt)

如果你需要找到的P2不仅要能构成可逆矩阵，还希望 P 是一个正交矩阵（这在很多情况下有额外的好处），那么可以使用施密特正交化过程。

步骤：

1. 从 P1 的基向量 ​\{v_1, \dots, v_k\} 开始，先将它们正交化，得到一组 W 的标准正交基 ​\{u_1, \dots, u_k\}。
2. 任意选取一个不属于子空间 W 的向量 ​w_{k+1}。（可以使用方法一中的筛选思想，找一个不能被 ​\{v_1, \dots, v_k\} 线性表示的标准基向量）。
3. 对 ​w_{k+1} 进行施密特正交化，即减去它在子空间 W 上的投影分量，得到 ​u_{k+1}。
4. 重复此过程，直到找到 n-k 个与 W 正交的向量，并将它们单位化，得到 ​\{u_{k+1}, \dots, u_n\}。
5. 此时，​\{u_1, \dots, u_n\} 是一组标准正交基，将它们作为列向量构成的矩阵 P 就是一个正交矩阵（因此必然可逆），并且 P1 和 P2 的列向量所张成的空间是正交的。

---

这在相似变换中意味着什么？

当你找到了这样的 P = [P1 | P2] 之后，你就可以计算新的矩阵 A' = P⁻¹AP。由于P1的列向量张成的空间 W 是A的不变子空间，这意味着：

• 对于P1中的任意列向量 ​v_j (其中 ​j \le k)，Avⱼ 的结果仍然在 W 空间内。
• 因此，Avⱼ 可以表示为 P1 中列向量的线性组合，而与 P2 中的向量无关。

这会导致 A' = P⁻¹AP 具有一个非常特殊的块结构：

• B 是一个 k x k 的矩阵，它表示线性变换 T 在子空间 W 上的作用。
• 0 是一个 (n-k) x k 的零矩阵。这块零的出现，正是因为 W 是不变子空间的直接结果。
• C 和 D 是另外两个子矩阵。

通过找到P2将基扩充，我们成功地将原矩阵A通过相似变换，变成了一个块上三角矩阵。

定理5：相似对角化的条件

一个n阶方阵A可相似对角化，等价于存在一个基 P = {p₁, p₂, ..., pₙ}，使得对于这个基中的每一个向量 pⱼ，由它的像 Apⱼ 所张成的一维子空间 span{Apⱼ} 都是A的一个不变子空间。这其实就是特征值与特征向量的概念了。每一个Pi都是一个特征向量，总共有n个线性无关的特征向量构成基。其实这是一句废话，如果你找不到n个线性无关的一维子空间，你根本就没办法将矩阵相似对角化。

定义17：特征值与特征向量

设 A 是一个 n×n 的方阵，p 是一个 n 维的非零列向量，而 λ 是一个标量。

如果它们满足以下方程：Ap=pλ

那么，我们就称：

• 标量 λ 为矩阵 A 的一个特征值 (Eigenvalue)。
• 非零向量 p 为矩阵 A 对应于特征值 λ 的一个特征向量 (Eigenvector)。
• 所谓特征值和特征向量就是一个一维不变子空间和它对应的系数了。

理解7：特征值与特征向量

我们从最抽象的线性空间出发，通过“基”和“坐标化”，成功地将抽象的“向量”和“线性映射”与具体的“坐标列向量”和“矩阵”对应起来。这让我们拥有了强大的计算工具。然而，一个线性变换在不同的基下会表现为不同的矩阵，有些矩阵复杂，有些则很简单。这就引出了我们的问题：如何为给定的线性变换，找到一个“最佳”的视角（即最佳的基），使得它对应的矩阵表示最为简洁？

1. 矩阵等价 (一般线性映射 ​A: V \to W)

• 关系: ​B = Q^{-1}AP。​A 和 ​B 代表同一个线性映射，但在不同的始空间基 (​P) 和终空间基 (​Q) 下。
• 最简形式: 可简化为 ​\begin{pmatrix} I_r & 0 \\ 0 & 0 \end{pmatrix}。
• 方法: 选择与映射的核 (Kernel) 和像 (Image) 空间相适应的基。
• 不变量: 矩阵的秩 (Rank)。

2. 矩阵相似 (线性变换 ​A: V \to V)

• 关系: ​B = P^{-1}AP。​A 和 ​B 代表同一个线性变换，但在同一个空间的不同基 (​P) 下。这是更强的关系。
• 简化工具: 寻找不变子空间——即被变换 ​A 映射到其自身的子空间。
• 理想形式: 对角矩阵。

3. 对角化与特征值

• 对角化的几何意义: 变换在选定的基方向上，作用仅仅是独立的伸缩。
• 条件: 每个基向量自身都必须张成一个一维不变子空间。
• 代数定义: 一个非零向量 ​\mathbf{p} 张成一维不变子空间的条件是 ​A\mathbf{p} = \lambda\mathbf{p}。
  • 特征向量 (​\mathbf{p}): 定义了变换的一个不变方向。
  • 特征值 (​\lambda): 是在该方向上的伸缩比例。
• 核心结论: 一个 ​n \times n 矩阵 ​A 可相似对角化，当且仅当它拥有 ​n 个线性无关的特征向量。这些特征向量构成的基，就是使变换矩阵对角化的最优基。