构建一个现代的大模型需要的基础知识
float32,BF16,BF8
| 格式 | 总位数 | 指数位数 (范围) | 尾数位数 (精度) | 核心用途与特点 |
|---|---|---|---|---|
| Float32 (FP32) | 32 | 8 | 23 | 高精度、高稳定性,但内存和计算成本高,混合训练的时候用它来更新梯度。 |
| BFloat16 (BF16) | 16 | 8 | 7 | 范围与FP32相同,牺牲精度换来巨大效率提升,现在的模型大部分矩阵运算使用这个精度就好。 |
| FP8 (E5M2/E4M3) | 8 | 5 / 4 | 2 / 3 | 极致的速度和内存效率,主要用于推理,用在训练上有些太难了,但是有一些尝试。 |
MFU
MFU 是 模型 FLOPs 利用率 (Model FLOPs Utilization) 的缩写。MFU = (实际达到的浮点数运算速度) / (硬件理论上的峰值浮点数运算速度)
第一步:计算模型的理论计算量 (Model FLOPs)
模型 FLOPs ≈ 6 × N × D
这里的变量分别是:
- N: 模型的参数量 (Number of parameters)。例如,GPT-3 是 175B (1750亿)。
- D: 该批次处理的 Token 总数 (Total tokens processed in the batch)。D = 批次大小 (Batch Size) × 序列长度 (Sequence Length)。
- 系数 6: 这是一个经验系数。它将计算量粗略地分为:
- 2N: 用于前向传播。每个参数大致对应一次乘法和一次加法(即一个 MAC 操作),约等于 2 FLOPs。所以是 2 * N * D。
- 4N: 用于后向传播。反向传播的计算量通常约是前向传播的 2 倍。所以是 4 * N * D。
- 两者相加,总计算量约等于 6 * N * D。
第二步:确定硬件的峰值性能 (Peak FLOPs)计算最终 MFU:
- 实际达到的 FLOPs = (模型 FLOPs) / (单步训练时间)
= (6 × N × D) / Time_per_step - MFU = (实际达到的 FLOPs) / (总峰值 FLOPs)
模型 FLOPs ≈ 6 × N × D
我们再来看看这个模型计算量的公式,让我们更深刻的理解他。
- FLOPs (Floating Point Operations): 指的是浮点数运算的总次数。注意,这不是FLOP/s(每秒浮点数运算次数,这是一个衡量硬件性能的速率单位)。这里的FLOPs是一个总计算量的计数,代表了完成整个训练任务需要执行多少次加、减、乘、除等基本数学运算。它是衡量训练成本的核心指标。
- N (Number of Parameters): 模型中可训练参数的总数量。这是衡量模型大小的指标。例如,GPT-3有1750亿(175B)个参数,LLaMA-7B有70亿(7B)个参数。
- D (Dataset Size in Tokens): 训练数据集包含的Token总数量。这是衡量数据规模的指标。例如,一个模型可能在1万亿(1T)个Token上进行训练。
1. 前向传播 (Forward Pass) 的计算量: ~2 × N
-
核心计算: 在Transformer模型中,绝大多数(超过95%)的计算都发生在矩阵乘法中,特别是在自注意力(Self-Attention)和前馈网络(Feed-Forward Network, FFN)层。
-
计算量估算: 对于一个拥有 N 个参数的模型,当一个Token通过模型进行一次前向传播时,它需要进行的浮点运算次数约等于参数数量的两倍。
-
为什么是2N?: 考虑一个最简单的矩阵乘法 y = Wx。如果 W 是一个 m × k 的矩阵,x 是一个 k × 1 的向量,那么计算 y 中的每一个元素都需要 k 次乘法和 k-1 次加法,总共是 2k-1 次运算,全部运算的成本为m(2k-1)->~2 mk-> ~2 × N。当我们将一个Token的向量表示(embedding)在模型的各个层之间传递时,它会与模型的权重矩阵相乘。通过对整个Transformer架构中的所有矩阵乘法进行复杂的加总和简化,业界得出了一个非常实用的经验法则:处理一个Token的一次前向传播,大约需要 2N 次FLOPs。
前向传播成本 ≈ 2 × N FLOPs / Token
2. 反向传播 (Backward Pass) ≈ 4N FLOPs
-
目的:根据模型的预测误差,计算出每个参数的梯度,以便更新和学习。
-
计算核心:反向传播的计算量大约是前向传播的两倍。这是因为它必须执行两个独立的、计算量相当的任务。
-
推导:我们基于**批处理(Batching)**的视角,并将总成本分摊到批次中的每一个样本上。
- 任务 A:计算权重梯度 (dL/dW)
- 目的:为模型学习提供方向,计算出每个权重需要调整多少。
- 操作:dL/dW = (dL/dY) * X^T。这是一个矩阵乘法。
- 平均成本/样本:≈ 2N FLOPs。
- 任务 B:计算输入梯度 (dL/dX)
- 目的:为传递误差到前一层,让整个网络协同学习。
- 操作:dL/dX = W^T * (dL/dY)。这是另一个矩阵乘法。
- 平均成本/样本:≈ 2N FLOPs。
- 任务 A:计算权重梯度 (dL/dW)
-
总成本:将两个任务的成本相加,得到反向传播的总成本。
FLOPs_backward ≈ FLOPs_taskA + FLOPs_taskB ≈ 2N + 2N = **4N **FLOPs / Token
3.推导一下4N怎么来的
我们以最简单的线性模型的矩阵乘法为例,加以推导。
第一步:定义维度
在实际的深度学习训练中,我们从不一次只处理一个样本。我们会将 B 个样本组合成一个批次 (Batch) 进行计算,以充分利用硬件的并行能力。这会改变我们输入的维度。
- W (权重矩阵): 它的维度保持不变,我们设为 (m, k)。
- 参数量 N = m × k
- x (单个输入向量): 维度为 (k, 1)。
- X (输入批次): 这是 B 个输入向量的集合。它的维度是 (k, B)。(我们将每个样本作为一列)
- Y (输出批次): 通过 Y = WX 计算得出。
- 维度: (m, k) @ (k, B) -> (m, B)。这很合理,B 个输入样本,每个产生一个 m 维的输出。
- dL/dY (上游传来的梯度): 它必须和 Y 的维度相同,所以是 (m, B)。
第二步:推导 dL/dW 的计算
现在,我们来计算 dL/dW,即任务1。
- 操作: 正确的梯度计算公式是 dL/dW = (1/B) * (dL/dY) * X^T。我们暂时忽略常数 1/B,因为它不影响FLOPs。核心操作是 (dL/dY) * X^T。
- **维度分析 **:
- dL/dY 的维度是 (m, B)。
- X 的维度是 (k, B),所以 X^T (X的转置) 的维度是 (B, k)。
- 执行矩阵乘法: (m, B) @ (B, k)
- 结果维度: 得到的 dL/dW 矩阵维度是 (m, k)。
- 计算FLOPs: 现在我们来计算 (m, B) @ (B, k) 这次标准矩阵乘法的计算量。
- 为了计算出结果矩阵中的一个元素,我们需要取 dL/dY 的一行(长度为 B)和 X^T 的一列(长度为 B)进行点积。
- 这个点积需要 B 次乘法和 B-1 次加法,总计 2B - 1 ≈ 2B FLOPs。
- 结果矩阵 dL/dW 总共有 m × k 个元素。
- 总FLOPs = (每个元素的计算量) × (元素总数)
= (2B) × (m × k)
= 2 × B × (m × k) - 代入 N: 因为 N = m × k,所以 总FLOPs = 2 × B × N。
- 得出结论:
- 为整个批次计算权重梯度的总计算量是 2BN。
- 那么,分摊到批次中每一个样本的平均计算量就是 (2BN) / B = 2N。
所以,FLOPs_task1 ≈ 2N 这个结论是完全正确的,但它的前提是基于批处理的平均计算成本。
第三步:推导 dL/dX (任务2)
为了完整性,我们也用同样的方法分析任务2。
- 操作: dL/dX = W^T * (dL/dY)
- 维度分析:
- W 是 (m, k),所以 W^T 是 (k, m)。
- dL/dY 是 (m, B)。
- 执行矩阵乘法: (k, m) @ (m, B)
- 计算FLOPs: 计算 (k, m) @ (m, B) 的FLOPs。
- 结果矩阵有 k × B 个元素。
- 每个元素需要 m 次乘法和 m-1 次加法,约 2m FLOPs。
- 总FLOPs = (k × B) × (2m) = 2 × B × (k × m)
- 代入 N: 总FLOPs = 2 × B × N。
- 结论: 分摊到每个样本的平均计算量也是 2N。
梯度运算
在进行推导之前,我们首先建立一个统一的坐标系。我们分析的是一个全连接层,它包含 m 个神经元,并正在处理一个由 B 个样本组成的批次。
-
权重矩阵
W(维度m, k):- 矩阵的第
i行 (W_i) 代表第i个神经元的权重向量。 - 矩阵中的元素
W_ik是第i个神经元连接到第k个输入特征的权重值。
- 矩阵的第
-
输入矩阵
X(维度k, B):- 矩阵的第
j列 (X_j) 代表第j个样本的k维输入特征向量。
- 矩阵的第
-
输出矩阵
Y(维度m, B):- 矩阵的第
j列 (Y_j) 是第j个样本经过所有m个神经元计算后得到的m维输出向量。 - 矩阵的第
i行 (Y_i) 是第i个神经元对所有B个样本分别计算后得到的输出值的集合。 - 矩阵中的元素
Y_ij是第i个神经元处理第j个样本后得到的单个标量输出。
- 矩阵的第
1. dL/dY: 上游梯度 —— 误差信号的接收
-
核心目标:
dL/dY是当前层反向传播计算的输入。它的目标是为当前层的每一个输出Y_ij,提供一个定量的、由网络后续部分计算得出的误差信号。 -
形式化定义与元素含义:
dL/dY是标量损失函数L对输出矩阵Y的梯度。其元素(dL/dY)_ij是偏导数∂L/∂Y_ij,它量化了总损失L相对于第i个神经元在处理第j个样本时的输出Y_ij的敏感度。- 符号表示
Y_ij相对于最优值的调整方向。 - 幅度表示
Y_ij对总损失L的影响程度。
- 符号表示
-
在反向传播中的角色:
dL/dY是一个结构化的误差矩阵,是当前层进行所有梯度计算的初始已知量。它将来自下游的、关于总损失的宏观信息,精确地归因到了当前层的每一个具体输出上。
2. (dL/dY) @ X^T 计算 dL/dW: 权重梯度 —— 参数优化的依据
-
核心目标: 计算
dL/dW的目标,是确定每一个独立权重W_ik(第i个神经元的第k个权重) 对总损失L的梯度,从而为参数优化提供依据。 -
链式法则的统一视角解读:
∂L/∂W_ik = Σ_j (∂L/∂Y_ij * ∂Y_ij/∂W_ik)
此公式的含义是:要计算第i个神经元的第k个权重W_ik的总梯度,必须将其在处理批次中所有B个样本时产生的影响进行累加。对于单个样本j,其影响由两部分相乘得到:∂L/∂Y_ij: 第i个神经元对该样本的输出Y_ij所对应的误差信号。∂Y_ij/∂W_ik = X_kj:Y_ij对W_ik的导数,等于该样本的第k个输入特征X_kj的值。
-
与矩阵运算的统一:
上述求和Σ_j ( (∂L/∂Y_ij) * X_kj ),是在所有样本j的维度上进行的。它在数学上精确对应于:dL/dY的第i行: 包含了第i个神经元在所有B个样本上的误差信号。X的第k行: 包含了第k个输入特征在所有B个样本上的激活值。- 这两个行向量的点积,就计算出了
(dL/dW)_ik。
因此,矩阵乘法(dL/dY) @ X^T是一种向量化的实现,通过一次运算即可计算出完整的权重梯度矩阵dL/dW。
-
在反向传播中的角色: 计算出的
dL/dW将被传递给优化器,用于执行参数更新(W_new = W_old - learning_rate * dL/dW)。这是模型学习过程的直接体现。
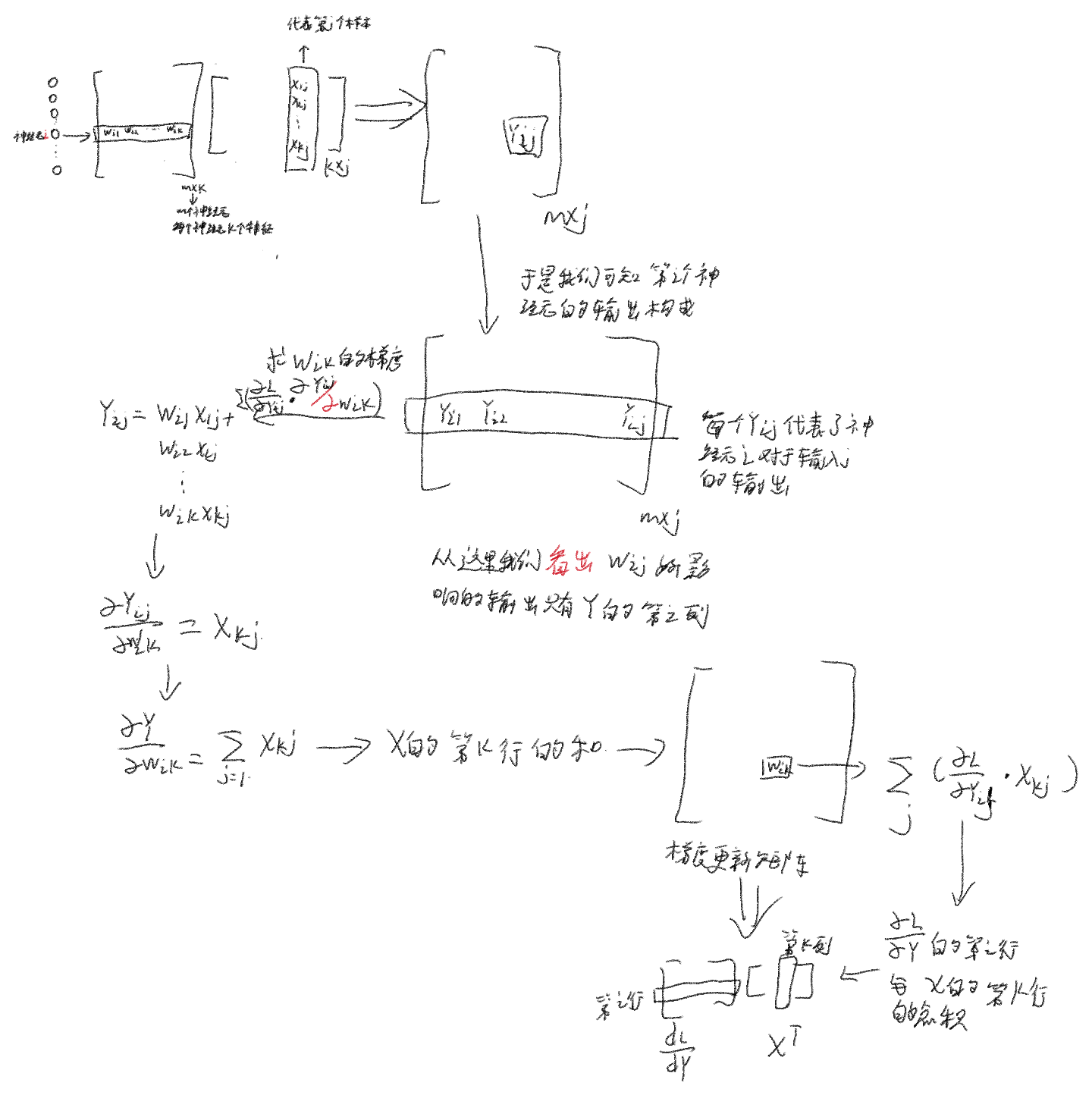
3. W^T @ (dL/dY) 计算 dL/dX: 输入梯度 —— 误差信号的传播
-
核心目标: 计算
dL/dX的目标,是将误差信号传播到网络的前一层。具体而言,是计算总损失L相对于当前层的每一个输入X_kj的梯度。 -
链式法则的统一视角解读:
∂L/∂X_kj = Σ_i (∂L/∂Y_ij * ∂Y_ij/∂X_kj)
此公式的含义是:第j个样本的第k个输入特征X_kj的信号被传递给了所有m个神经元。因此,要计算X_kj对总损失的全部间接影响,必须将其通过每一个神经元i传播的误差贡献进行累加。对于单个神经元i,其贡献由两部分相乘得到:∂L/∂Y_ij: 第i个神经元对该样本的输出Y_ij所对应的误差信号。∂Y_ij/∂X_kj = W_ik:Y_ij对X_kj的导数,等于连接它们的权重W_ik。
-
与矩阵运算的统一:
上述求和Σ_i ( (∂L/∂Y_ij) * W_ik ),是在所有神经元i的维度上进行的。它在数学上精确对应于:dL/dY的第j列: 包含了第j个样本从所有m个神经元接收到的误差信号。W的第k列: 包含了连接第k个输入到所有m个神经元的权重。- 这两个列向量的点积,就计算出了
(dL/dX)_kj。(这等价于W^T的第k行与dL/dY的第j列的点积)。
因此,矩阵乘法W^T @ (dL/dY)通过一次运算,即可将所有输出端的误差,按照权重重新分配并汇集到输入端。
初始化
| 特性 | Xavier 初始化 (Glorot) | He 初始化 (Kaiming) |
|---|---|---|
| 核心思想 | 同时考虑前向和反向传播,维持信号方差稳定 | 主要考虑前向传播,弥补 ReLU 导致的信息损失 |
| 方差公式 | Var(W) = 2 / (n_in + n_out) | Var(W) = 2 / n_in |
| 适用激活函数 | Tanh, Sigmoid | ReLU 及其所有变体 |
| 提出时间 | 2010年 | 2015年 |
| 正态分布 | 均值为 0,标准差为 sqrt(2 / (n_in + n_out)) 的高斯分布中采样。 | 均值为 0,标准差为 sqrt(2 / n_in) 的高斯分布中采样。 |
| 均匀分布 | [-limit, limit] 的均匀分布中采样,其中 limit = sqrt(6 / (n_in + n_out)) | [-limit, limit] 的均匀分布中采样,其中 limit = sqrt(6 / n_in) |
