A foundation model for the Earth system论文阅读笔记

动机

现有的研究（包括pangu-weather， Fourcastnet， GraphCast...）仍聚焦于全球中期天气预报（7天以内，0.25° 分辨率）。没有系统扩展到海洋动力学，大气建模，热带气旋以及高分辨率天气预测等领域。于是就像GPT一样，他们希望构建一个系统的地球基础模型，然后使用微调对于具体的任务进行适配。

方法

模型总体结构

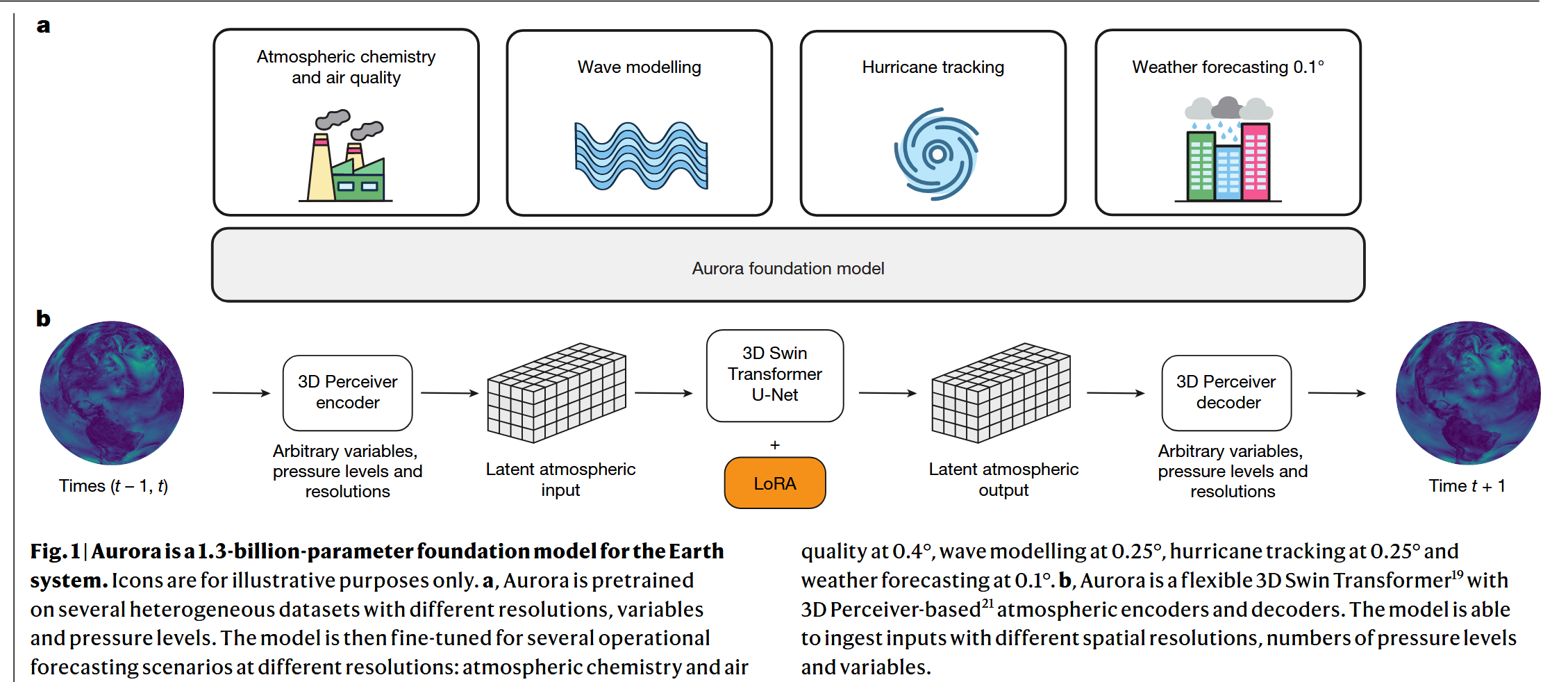
image-20251014205816110

模块 作用 工作细节
3D Perceiver Encoder 将各种不同格式的输入数据转换成一个标准化的、统一的内部表示 将输入的地球系统变量（如温度、风速）视为一系列2D图像，并将其分割成小“图块”(patches)。使用Perceiver 模块，将多个物理气压层的信息“压缩”到固定的几个“潜在”层中。同时，编码器还加入了时间、经纬度位置和图块物理面积等编码信息。
3D Swin Transformer U-Net 模拟地球系统状态随时间的演变 使用3D Swin Transformer模块，它在局部“窗口”内计算注意力，模拟了物理世界中局部区域相互作用的特性，计算效率远高于传统的全局注意力。使用U-Net 结构，这种“先下采样再上采样”的对称结构，使得模型能够在多个空间尺度上捕捉和处理信息。
3D Perceiver Decoder 将处理器输出的标准化内部表示转换回用户需要的具体物理预测结果 它同样使用 Perceiver 模块，将处理后的“潜在”层信息“解压缩”到任意指定的目标物理气压层上，并最终解码成具体的变量预测图。

具体模块

Perceiver 模块

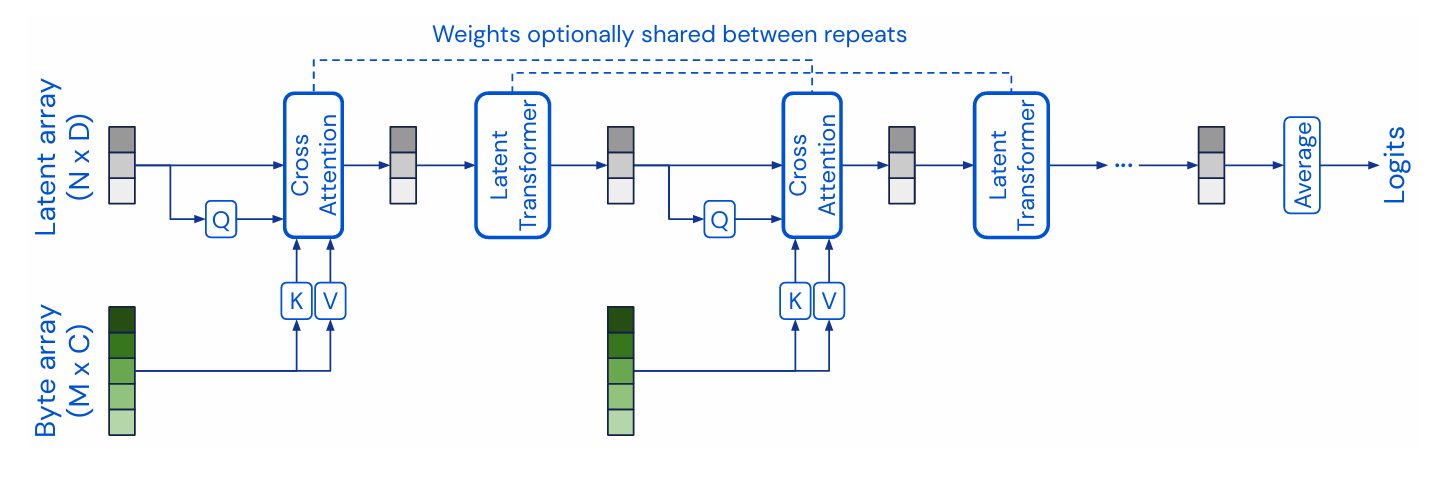
image-20251014212557644

以下是这张图的分步解析：

首先，我们识别图中的两个主要数据流：

  1. Byte Array (M x C)：这是模型的原始输入，位于图的底部。
    • M 代表输入的元素数量。这个数字可以非常大，比如一张 224x224 图片的像素总数（M ≈ 50,000）。
    • C 代表每个元素的特征维度。例如，对于一个像素，C 可能包括 R, G, B 值以及其位置编码的维度。。
  2. Latent Array (N x D)：这是模型的核心处理单元，是信息瓶颈，位于图的顶部。
    • N 是隐式向量的数量。这个数字是固定的、相对较小的超参数（例如 N=512），远小于 M。
    • D 是每个隐式向量的特征维度。

整个流程是迭代进行的，我们先分析第一个“重复”（repeat）块。

第1步：首次信息提炼 (First Cross-Attention)

  • 生成 Query (Q)：隐式数组 (Latent Array) 被送入一个线性层，生成 Q 向量。Q 的维度是 (N, D_attn)。你可以把这 N 个隐式向量想象成 N 个“问题”或“查询请求”。
  • 生成 Key (K) 和 Value (V)：字节数组 (Byte Array) 被送入两个不同的线性层，分别生成 K 和 V 向量。K 和 V 的维度分别是 (M, D_attn) 和 (M, D_val)。你可以把 K 和 V 想象成输入数据提供的“目录”和“内容”。
  • 非对称注意力计算：在 Cross-Attention 模块中，模型计算 Attention(Q, K, V)。
    • Q 来自小数组，K 和 V 来自大数组，这就是“非对称”的来源。
    • 计算过程是：N 个查询 (Q) 与 M 个键 (K) 进行点积，得到一个 (N, M) 的注意力分数矩阵。这个矩阵的每一行表示一个隐式查询对所有 M 个输入元素的关注程度。
    • 然后，用这个注意力分数矩阵对 M 个值 (V) 进行加权求和。
  • 输出：Cross-Attention 模块的输出是一个新的、更新后的隐式数组，其维度仍然是 (N, D)。这个新的数组已经吸收了来自 Byte Array 的初步信息，可以看作是原始数据的一个高度浓缩的“摘要”。

第2步：首次信息处理 (First Latent Transformer)

  • 上一步得到的“摘要”（更新后的 Latent Array）被送入一个标准的 Latent Transformer 模块。
  • 在这个模块内部，进行的是 自注意力 (Self-Attention)。也就是说，Q, K, V 全部都来自于这个 (N, D) 的隐式数组。
  • 目的：在已经提炼出的信息内部进行复杂的推理、比较和特征融合。由于所有计算都在 N x N 的小维度上进行，这个过程计算成本非常低，且可以做得非常深。
  • 输出：经过 Latent Transformer 处理后，我们得到一个经过深度处理、信息更加丰富的 Latent Array。

图中的流程展示了上述“Cross-Attention -> Latent Transformer”模块对的重复。

  • 第二次迭代：第一次迭代的输出（那个经过深度处理的 Latent Array）现在成为了第二次 Cross-Attention 模块的新 Query (Q)。
  • 关键洞见：这个新的 Q 不再是初始的随机向量，它已经包含了对整个输入的初步理解。因此，当它再次去查询同样的 Byte Array (Byte Array 依然提供 K 和 V) 时，它可以提出更“有针对性”、“更深刻”的问题，从而提炼出更细节或更全局的信息。
  • 这个过程可以重复多次（图中用 ... 表示），每一次迭代，Latent Array 都变得更加“知情”，对原始输入的理解也愈发深刻。

图顶部的虚线箭头指出了一个重要的实现细节：

  • 在不同的“重复”块之间，Cross-Attention 模块和 Latent Transformer 模块的权重（即线性层和注意力机制的参数）可以共享。
  • 如果共享权重，整个架构就非常像一个在深度维度上展开的循环神经网络 (RNN)。其中，Latent Array 扮演着 RNN 的隐藏状态 (hidden state)，而 Byte Array 是每一“步”都保持不变的静态输入。这种方式使得模型非常参数高效。

Swin Transformer模块

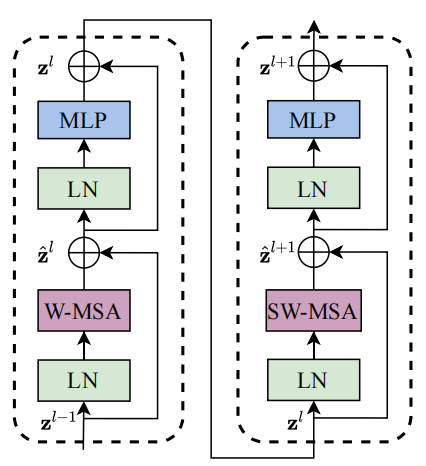
image-20251014222259064

Swin Transformer的核心目标是让Transformer模型能像卷积神经网络（CNN）一样，作为计算机视觉领域的通用骨干网络（general-purpose backbone）。它需要解决标准Vision Transformer (ViT) 的两大问题：

  1. 计算复杂度：ViT的自注意力是全局计算的，其计算量与输入图像块（patch）数量的平方成正比 O((HW)^2)。这使得它难以处理高分辨率图像或应用于需要密集预测（如分割）的任务。
  2. 尺度不变性：ViT在所有层都保持相同的特征图分辨率，缺乏像CNN那样的层级式特征表示（Hierarchical Representation），这对于捕捉不同尺度的视觉目标是不利的。

Swin Transformer通过 「窗口化自注意力 (W-MSA)」 和 **「移动窗口化自注意力 (SW-MSA)」以及[PatchMerging]**来解决的VIT的问题。

过程解析：W-MSA 与 SW-MSA 的交替

Swin Transformer的基础构建块由两个连续的Transformer Block组成。这两个Block的区别仅在于其注意力模块，一个使用W-MSA，另一个使用SW-MSA。

第 l 层：窗口化多头自注意力 (Window-based Multi-head Self-Attention, W-MSA)

  1. 特征图分区 (Window Partitioning)：不同于ViT在整个特征图上计算注意力，W-MSA首先将输入的特征图（假设尺寸为 h x w）均匀地划分为若干个不重叠的 窗口（Window）。例如，如果窗口大小设置为 M x M，那么特征图会被分成 (h/M) x (w/M) 个窗口。
  2. 局部注意力计算 (Local Self-Attention)：接下来，模型在 每个窗口内部 独立地执行标准的多头自注意力（Multi-head Self-Attention）。这意味着，一个图像块（patch）只会与它所在窗口内的其他图像块计算注意力关系。
  3. 结果：由于注意力被限制在固定的、不重叠的窗口内，计算量大大降低。然而，这也带来了一个明显的问题：不同窗口之间完全没有信息交互，模型的感受野被限制在了小窗口内。

第 l+1 层：移动窗口化多头自注意力 (Shifted Window Multi-head Self-Attention, SW-MSA)

为了解决W-MSA中窗口间信息隔离的问题，紧随其后的SW-MSA引入了一个巧妙的“移动”机制。

img

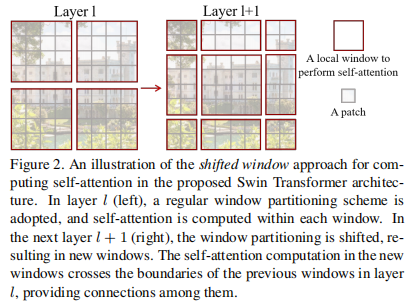
1.特征图循环移位 (Cyclic Shift)：如图 2 所示，在进行窗口分区之前，SW-MSA首先将第 l 层输出的特征图向左上角方向进行循环移位。移位的距离通常是窗口大小的一半，即 (⌊M/2⌋, ⌊M/2⌋)。

img

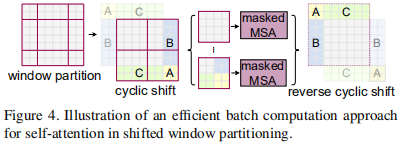
2.重新分区与注意力计算：对移位后的特征图，采用与W-MSA完全相同的窗口分区策略。由于移位操作，新的窗口会包含来自上一层中不同窗口的图像块。例如，一个 2x2 的新窗口可能包含了上一层 4 个不同窗口的邻接部分。比如说窗口5，你可以看到他的组成来自原来4个窗口的拼接。

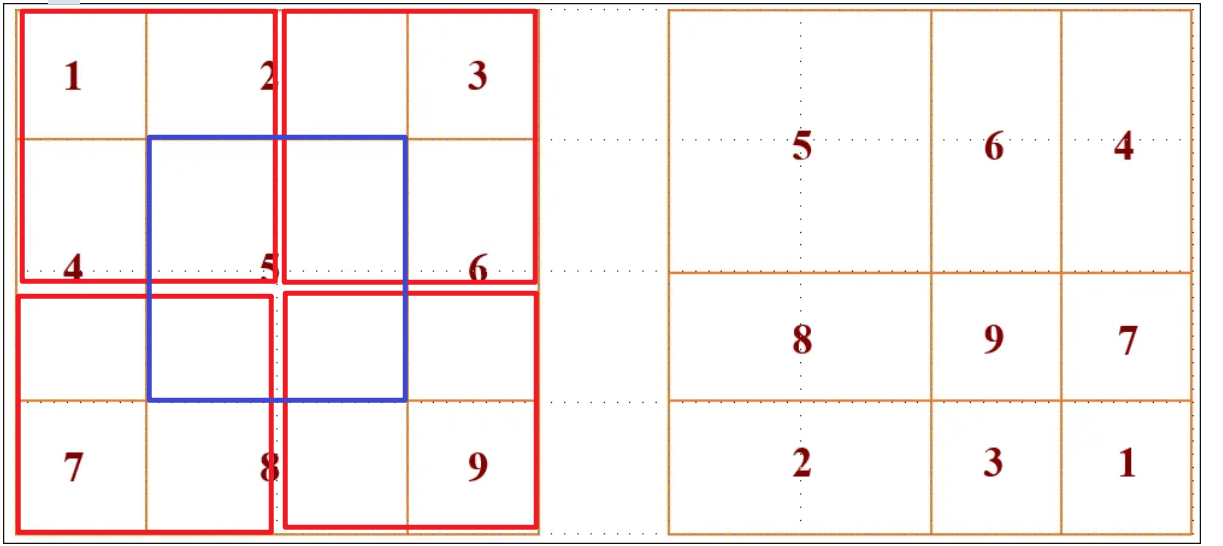
image-20251014233620248

3.建立跨窗口连接：当在这个新的、混合了来源的窗口内计算自注意力时，就自然而然地实现了跨窗口的信息流动。

4.注意力计算：现在我们面临一个新的问题：在这些新“凑”出来的窗口里，有些 patch 在原始图像上是相邻的，我们希望它们之间计算注意力；而有些 patch 只是因为循环移位被凑到了一起，它们在原始图像上相距很远，我们不希望它们之间计算注意力。比如说6和4拼接出来的新的窗口，6和4内部的patch 在原本是相邻的，所以我们希望他们计算注意力，但是6和4之间在原本是不相邻的，他们原本在图像的两边，只不过因为循环移位导致他们凑到了一起，所以我们不希望他们计算注意力。

5.掩码：于是为了解决上面的问题我们引入了 masked MSA 机制。例如， 6 号 / 4 号子窗口共由 4 个 patch 构成一个正方形区域，如下所示，故应计算出 4×4 注意力图。

img

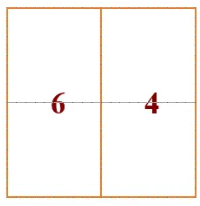
为避免各不同的子窗口注意力计算发生混叠，合适的注意力掩码图应如下所示：

img

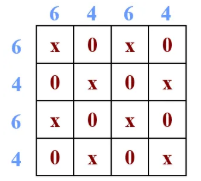
再例如，9 号 / 7 号 / 3 号 / 1 号子窗口共由 4 个 patch 构成一个正方形区域，如下所示：

img

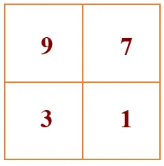
同理，合适的 掩码图应如下所示：

img

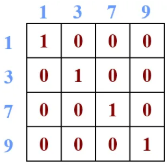
6.相对位置编码：此处作者还引入了相对位置编码。从论文中提供的公式，这个相对位置的偏执是加在softmax之前的：

Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{(}d)}+B)V

img

img

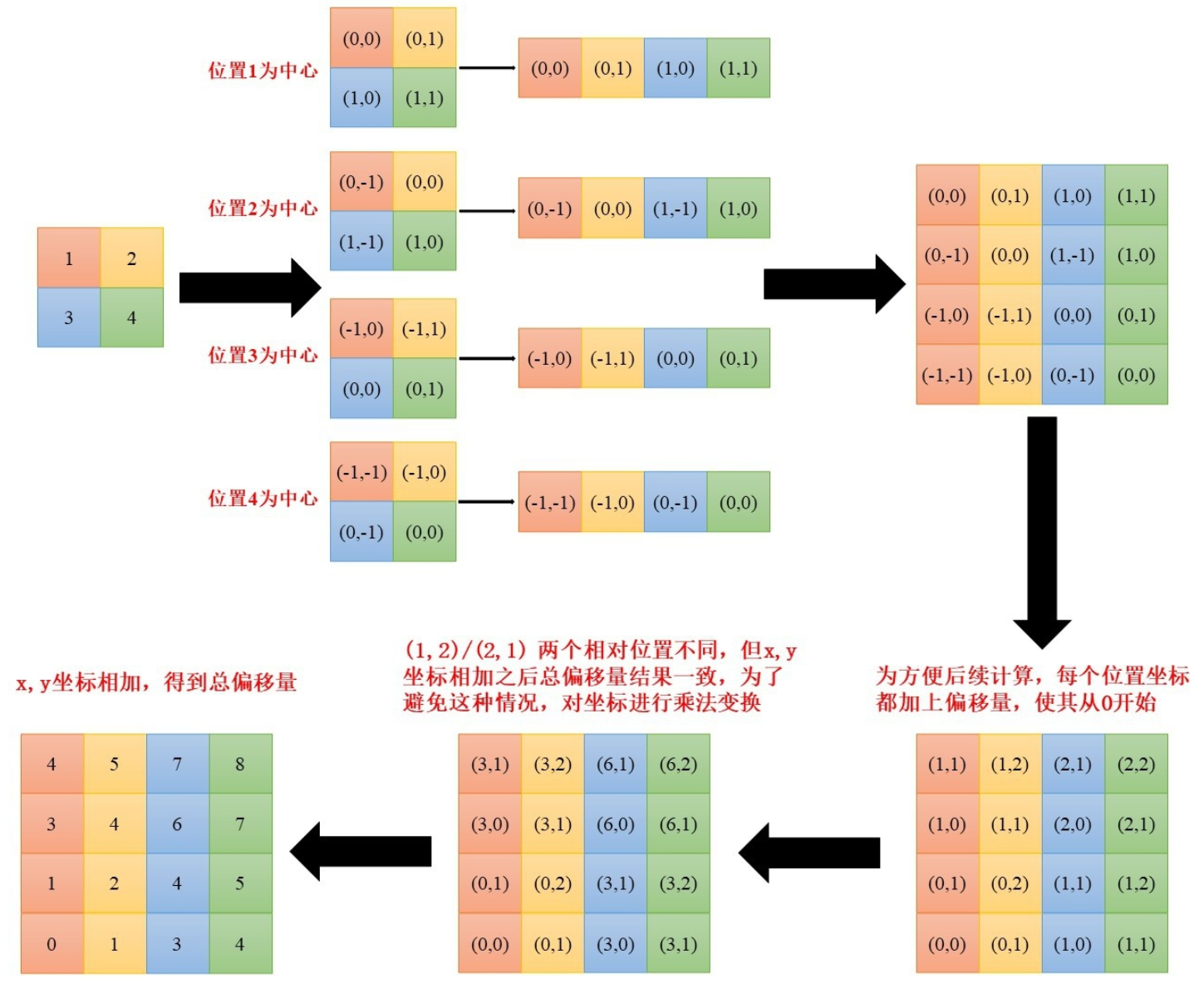
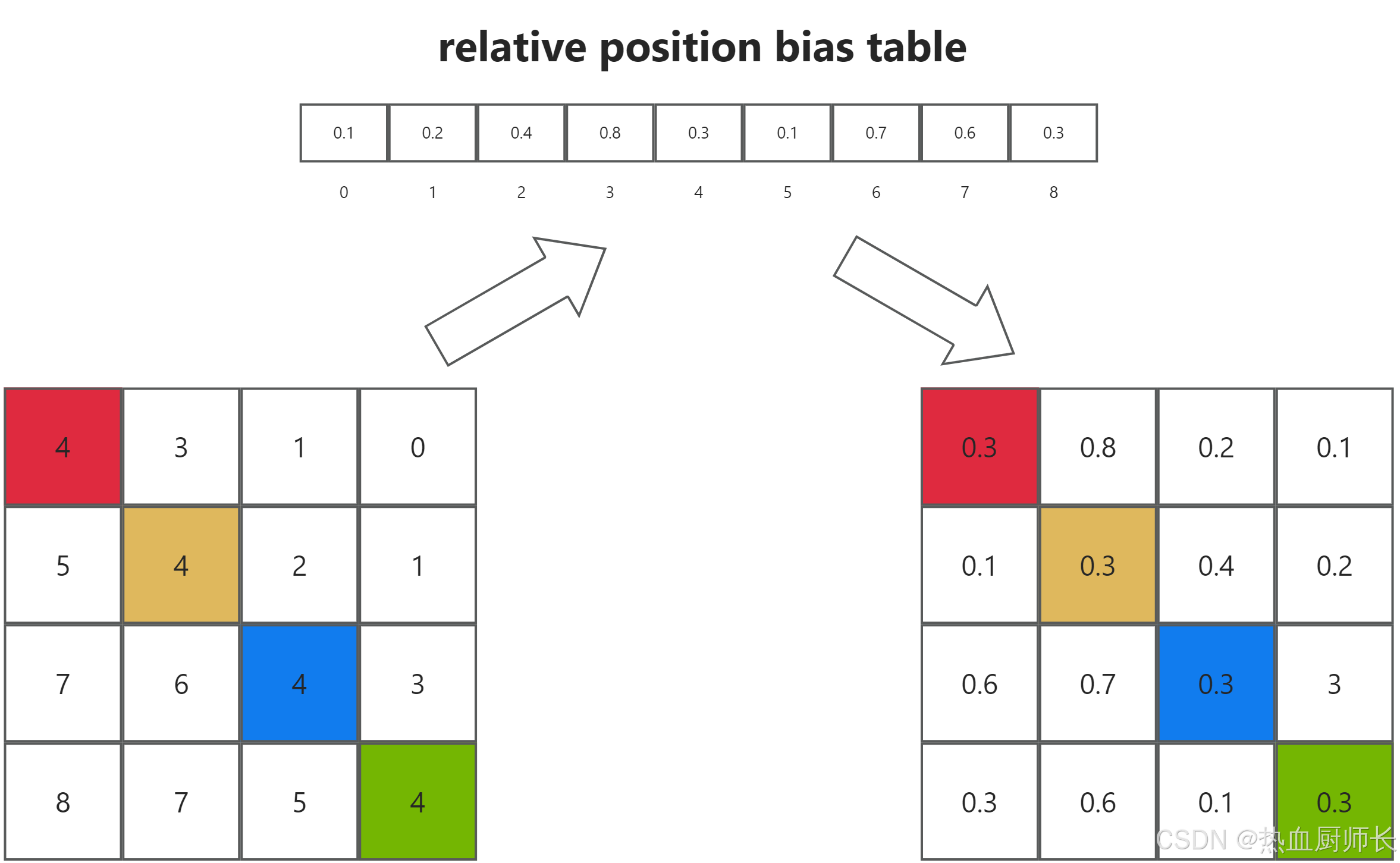
注意这一步，看起来可能有点奇怪，为什么会查表然后直接相加呢，这里其实是和注意力机制的计算有关。我们都知道自注意力的计算是下面这样的。

image-20251015011808824

然后我们将这个矩阵和上面这个矩阵重叠放置一下，你就会发现（1，3）所在的位置就是“1”和“3”之间的相对位置“1”，所以“1”也就是代表着3在1的下方。同样的，我们看位置编码矩阵中的另一个“1”在第二行的第四列，他代表着4在2的下方，那么，现在我们看以2为中心的相对位置编码矩阵，你会发现4就是再2的下方，并且如果你把相对位置看成一个箭头的话4->2和3->1的方向和大小是相同的，所以上面的理解是正确的，即位置编码矩阵中每一个独特的数字代表着一个独特的相对位置，比如上，下，左，右，左上，左下等等。让我们再回过头来看第二步对于相对位置的矩阵进行展开，思考一下，为什么要这样拼接成矩阵。现在按照上面的理解，以第二行为例，你会看到展开后的矩阵的第二行正好就是以2为中心，其他patch相对与2的位置。注意力矩阵计算的第二行计算的也是2和其他patch的注意力分数。

过程解析：PatchMerging

PatchMerging 是 Swin Transformer 中的一种下采样操作，但是不同于池化，这个相当于间接的（对H和W维度进行间隔采样后拼接在一起，得到H/2，W/2，C/4），目的是将输入特征图的空间维度（即高和宽）逐渐减小，同时增加通道数，从而在保持计算效率的同时获得更高层次的特征表示。它是下采样的过程，但与常规的池化操作不同，PatchMerging 通过将相邻的 patch 拼接在一起，并对拼接后的特征进行线性变换，从而实现下采样。具体来说，我们对于原始图像进行规律性地采样之后我们得到了一个新的张量，其维度为 (B, H/2, W/2, 4C)，之后我们应用一个全连接层。这个全连接层的输入维度是 4C，输出维度通常设置为 2C，最终输出的张量维度为 (B, H/2, W/2, 2C)得到了不同尺度的特征图。

img

参考：

(29 封私信 / 80 条消息) 【深度学习】深刻理解Swin Transformer - 知乎

狗都能看懂的Swin Transformer的讲解和代码实现-CSDN博客

【深度学习】详解 Swin Transformer (SwinT)-CSDN博客

编码

1. 位置编码 (Positional Encoding)

  • 目的: 告诉模型每个数据“图块”(patch) 在地球上的绝对地理位置。
  • 被编码的值 (x): 每个图块中心的平均纬度和平均经度。注意，它不是图块的索引 (i, j)，而是真实的地理坐标。
  • 实现细节:
    1. 将平均经度和维度放入傅里叶编码公式中得到编码向量。
    2. 两者拼接成一个 D 维的编码向量。前 D/2 维用于编码纬度。后 D/2 维用于编码经度。
    3. 论文中为位置编码设置的 λ_min = 0.01，λ_max = 720 (度)。这个范围意味着编码器既能分辨出非常小的位置差异（0.01度级别），也能理解全球范围的宏观位置关系（地球一圈是360度）。

2. 尺度编码 (Scale Encoding)

  • 目的: 告诉模型每个图块代表的真实物理面积有多大。这是处理多分辨率数据源（如0.1°的HRES和0.75°的CAMS）的关键。
  • 被编码的值 (x): 每个图块在地球表面上的真实面积 (Area)，单位是平方千米。
  • 实现细节:

    1. 论文中给出了计算球面上一个矩形区域面积的公式：

      A = R^2 (\sin(\phi_2) - \sin(\phi_1))(\theta_2 - \theta_1)

      其中 R 是地球半径，φ 是纬度，θ 是经度。

    2. 这个计算出的面积 A 就是被送入傅里叶特征编码公式的 x。

    3. 效果: 一个来自高分辨率数据集（如0.1°）的图块，其面积 A 会很小，得到一个编码；一个来自低分辨率数据集（如0.75°）的图块，其面积 A 会大很多，得到一个截然不同的编码。这样模型在处理这个图块的特征时，就能知道：“这个特征代表了一片小区域的精细信息”或“这个特征代表了一大片区域的平均信息”。

3. 层级编码 (Level Encoding)

  • 目的: 告诉模型每个大气变量数据所在的垂直高度。
  • 被编码的值 (x): 大气压强的数值 (单位: hPa)。例如，1000, 850, 500 等。
  • 实现细节:
    1. 对于大气变量（如风、温度），直接将它们所在的压强层数值（比如 500）作为 x 进行傅里叶编码。
    2. 特殊情况: 对于地表变量（如2米气温、海平面气压），它们没有压强层的概念。论文提到，模型会为所有地表变量使用一个单独的、可学习的向量 (a fully-learned vector) 作为它们的层级编码。这个向量就像一个特殊的标签，告诉模型：“这些数据都来自地表”。

4. 时间编码 (Time Encoding)

  • 目的: 告诉模型每个数据切片发生的绝对时间，以便学习日变化、周模式和季节性趋势。
  • 被编码的值 (x): 从一个固定起点（通常是1970年1月1日00:00 UTC）到当前时间的总小时数。这是一个巨大的整数。
  • 实现细节:
    1. 将这个总小时数作为 x 进行傅里叶编码。
    2. 论文中为时间编码设置的 λ_min = 1 (小时)，λ_max 约等于一年的总小时数 (365.25 * 24)。
    3. 这个参数选择非常巧妙：
      • λ_min = 1 意味着编码器的高频部分对小时级的变化非常敏感，有助于捕捉日内循环（例如，午后气温最高）。
      • λ_max 接近一年，意味着编码器的低频部分能捕捉到季节性变化。
      • 介于两者之间的波长则可以自然地捕捉到周、月等模式。